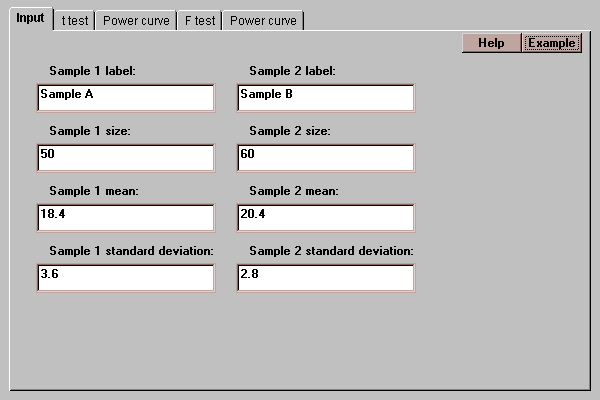
This statlet tests hypotheses about the means and standard deviations of two normal distributions. The tabs are:

To use this statlet, enter information about your data:
Sample labels - names to be displayed on the output.
Sample sizes - the number of observations in the samples.
Sample means - the means of the samples.
Sample standard deviations - the standard deviations of the samples.
This tab shows the result of a hypothesis test concerning the difference between the means:
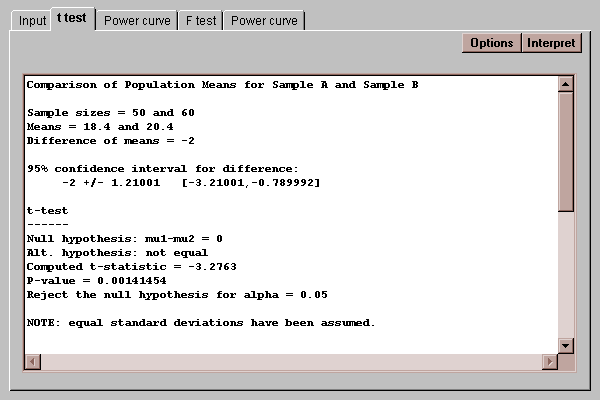
It shows:
Summary statistics.
A confidence interval for the difference between the means.
The result of a t-test run to test a hypothesis about the difference between the population means.
Use the Options button to specify the hypotheses to be tested. If the P-value is less than the alpha risk which you specify, you should reject the null hypothesis at the corresponding significance level.
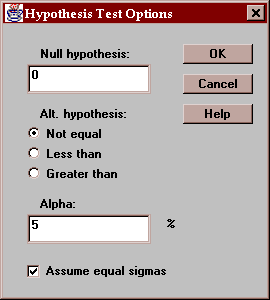
Enter:
Null hypothesis - the value of the mean difference specified by the null hypothesis.
Alt. Hypothesis - select a two-sided test (~=) or a one-sided test.
Alpha - the probability of a Type I error, which is a situation where a true null hypothesis is incorrectly rejected. Typical values for alpha are 10%, 5%, and 1%. The confidence interval is also affected by this setting and uses a confidence level equal to (100-alpha)%.
Assume equal sigmas - whether to assume that the samples come from populations with the same standard deviation.
This tab shows the power curve for the t test:
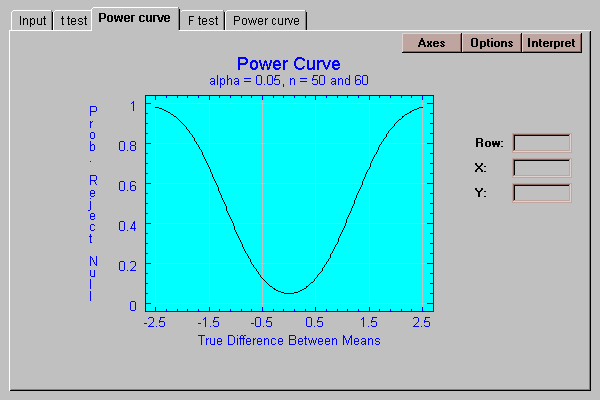
The power curve shows the probability of rejecting the null hypothesis as a function of the true difference between the population means.
Same as previous tab.
This tab shows the result of a hypothesis test concerning the ratio of the variances:
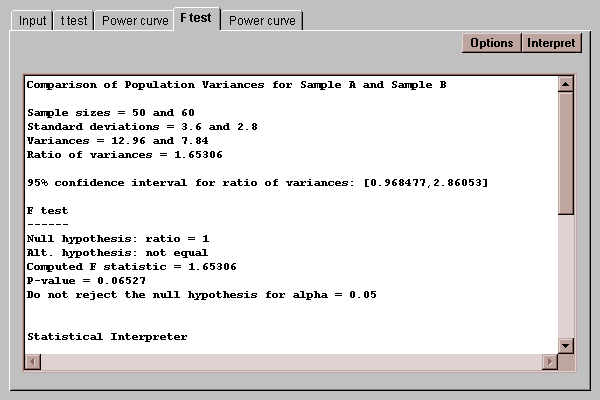
It shows:
Summary statistics.
A confidence interval for the ratio of the variances.
The result of an F test run to test a hypothesis about the ratio of the population variances.
Use the Options button to specify the hypotheses to be tested. If the P-value is less than the alpha risk which you specify, you should reject the null hypothesis at the corresponding significance level.

Enter:
Null hypothesis - the value of the ratio specified by the null hypothesis (usually 1.0).
Alt. Hypothesis - select a two-sided test (~=) or a one-sided test.
Alpha - the probability of a Type I error, which is a situation where a true null hypothesis is incorrectly rejected. Typical values for alpha are 10%, 5%, and 1%. The confidence interval is also affected by this setting and uses a confidence level equal to (100-alpha)%.
This tab shows the power curve for the F test:
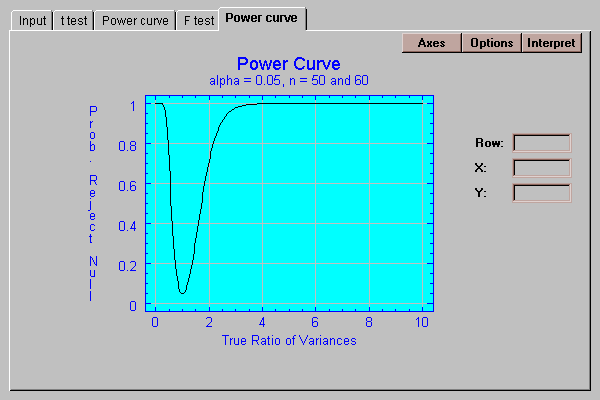
The power curve shows the probability of rejecting the null hypothesis as a function of the true ratio of the population variances.
Same as previous tab.