p-value Approach
|
Null & Alternative Hypothesis |
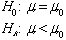
|
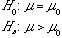
|
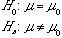
|
|
Significance Level Of the Test |
a |
a |
a |
|
Test Statistics |
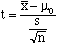
|
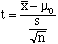
|
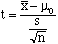
|
|
p-value |
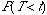
Table VI with d.f.=n-1 |
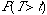
Table VI with d.f.=n-1 |
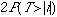
Table VI with
d.f.=n-1 |
|
Decision |
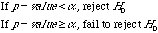
|

If you have been given or calculated the sample mean and
sample
standard deviation together with the sample size you can use the
Statlets window
presented below.
ACTIVITY
Some quality control experiments require destructive
sampling
(i.e., the test to determine whether the item is defective destroys
the
item) in order to measure some particular characteristics of the
product. The
cost of desctructive sampling often dictates small samples. Suppose a
manufacturer
of printers for personal computers wishes to estimate the mean number of
characters
printed before the printhead fails. The printer manufacturer tests
n
= 15 printheads and records the number of characters printed until
failure for
each. These 15 measurements yield a mean of 1.24 and a standard
deviation of
0.19 9in millions of characters). Suppose that the competitor's printers
has
a mean of 1.30 (in millions) for the number of characters printed before
the
printhead fails.
a. Test the hypothesis that mean number of
characters printed
before the printhead fails for this manufacturer is different than its
competitor.
Use the significance level 0.05.
- Step 1: Make sure that "Input"
menu option is selected.
- Step 2: Type "Number"
in the "Data label"
box.
- Step 3: Type "15"
in the "Sample size"
box.
- Step 4: Type "1.24"
in the "Sample mean"
box.
- Step 5: Type "0.19"
in the "Sample standard
deviation"
box.
- Step 6: Select the "t
test"
from menu options.Caution: Do not use the
output
yet.
- Step 7: Click
on the "Options"
button on the upper right hand side of the
window.
- Step 8: On
the
window that pops up, type the value of the mean specified in you null
hypothesis.
That is 1.3 in this
case.
- Step 9: Select
your alternative hypothesis. For this question the alternative
hypothesis
is two sided (we are interested whether the mean is different or
not). Therefore
select "Not
equal".
- Step 10: Type the significance level of the test. In this
case it
is "5.0"
- Step 11: Click
on the "OK" button.
The output will include: Sample size, Mean, Standard deviation, a 95%
confidence
interval for the population mean, and the result of the test.
b. Test the hypothesis that mean number of characters printed
before
the printhead fails for this manufacturer is less than its
competitor. Use the
significance level 0.05.
- Step 1: Make sure that "Input"
menu option is selected.
- Step 2: Type "Number"
in the "Data label"
box.
- Step 3: Type "15"
in the "Sample size"
box.
- Step 4: Type "1.24"
in the "Sample mean"
box.
- Step 5: Type "0.19"
in the "Sample standard
deviation"
box.
- Step 6: Select the "t
test"
from menu options.Caution: Do not use the
output
yet.
- Step 7: Click
on the "Options"
button on the upper right hand side of the
window.
- Step 8: On
the
window that pops up, type the value of the mean specified in you null
hypothesis.
That is 1.3 in this
case.
- Step 9: Select
your alternative hypothesis. For this question the alternative
hypothesis
is one sided (we are interested whether the mean is less). Therefore
select
"Less than".
- Step 10: Type the significance level of the test. In this
case it
is "5.0"
- Step 11: Click
on the "OK" button.
The output will include: Sample size, Mean, Standard deviation,
one-sided 95%
confidence interval for the population mean, and the result of the
test.
c. The manufacturer advertises that mean number of characters
printed
before the printhead fails for their printer is 1.4 (in million). What
would
be your response?
- Step 1: Make sure that "Input"
menu option is selected.
- Step 2: Type "Number"
in the "Data label"
box.
- Step 3: Type "15"
in the "Sample size"
box.
- Step 4: Type "1.24"
in the "Sample mean"
box.
- Step 5: Type "0.19"
in the "Sample standard
deviation"
box.
- Step 6: Select the "t
test"
from menu options.Caution: Do not use the
output
yet.
- Step 7: Click
on the "Options"
button on the upper right hand side of the
window.
- Step 8: On
the
window that pops up, type the value of the mean specified in you null
hypothesis.
That is 1.4 in this
case.
- Step 9: Select
your alternative hypothesis. For this question the alternative
hypothesis
is one sided (we are interested whether the mean is less). Therefore
select
"Less than".
- Step 10: Type the significance level of the test. In this
case it
is "5.0"
- Step 11: Click
on the "OK" button.
Note the p-value of this test and respond to the question.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
