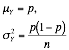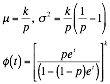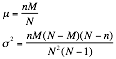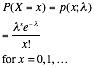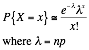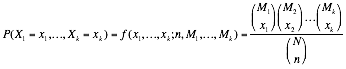Discrete Probability Distributions

Name	Experiment	Probability Mass Function (pmf), p(x)	Mean, Variance, Moment Generating Function	Comments
Discrete Uniform	Equally likely k different values
Bernoulli	• two possible outcomes	, x=0,1
Binomial	• two possible outcomes • fixed number of trials (n) • is fixed from trail to trial • independent trials	X=the number of successes out of n trials , x=0,1,…,n		• Let , then
Negative Binomial	• two possible outcomes • no fixed number of trials • is fixed from trail to trial • independent trials	X=the number of trials at which the kth success occurs. x=k,k+1,…		• If k=1 then it is called a geometric distribution. This distribution is memoryless. • For the geometric distribution
Hypergeometric	• N individuals in the population • two possible outcomes M=number of successes in the population • n individuals are selected without replacement	X=the number of successes out of n trials		• used when we sample without replacement
Poisson	• counts number of events in one unit • probability that an event occurs in one unit is same for all units • the number of events in units are independent	X=the number of times an event occurs in one unit		• Poisson Approximation to Binomial If X has Bin(n,p)
Multinomial	• k possible outcomes • fixed number of trials (n) • is fixed from trail to trial • independent trials	XI=outcomes of the ith kind.
Multivariate Hypergeometric	• N individuals in the population • k possible outcomes Mi=number of kind i in the population • n individuals are selected without replacement	XI=outcomes of the ith kind.