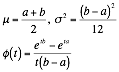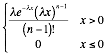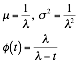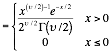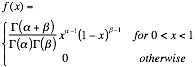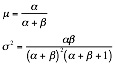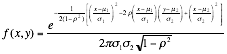Continuous Probability Distributions

Name	Probability Density Function (pdf), f(x)	Mean, Variance, Moment Generating Function		Comments
Uniform over (a, b)				• • non-informative, randomness distribution
Gamma parameters				• Very rich family with different shapes
Exponential parameters				• Gamma with n=1 • (survival function) • memoryless property
Chi-square parameter	(nu) is called the degrees of freedom			• Gamma with
Beta parameters				• A good model for proportions (Bayesian inference)
Normal parameters	Standard Normal m=0, s=1			• Bell shaped curve • To find a normal probability use the Table 2.3 on page 81 • If has then has • Normal approximation to binomial. Let X has Binom(n,q). Make the continuity correction and use the fact that
Bivariate Normal	Circular normal distribution r=0, s1=s2		• If X and Y have a bivariate normal distribution then 1. Y given X=x has a normal distribution with 2. X given Y=y has a normal distribution with 3. X and Y are independent iff r=0.