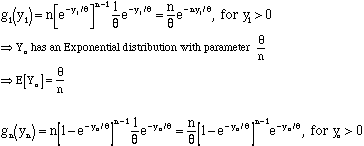INTRODUCTION TO MATHEMATICAL STATISTICS

MATH. 2611

SOLUTIONS TO THE THIRD MIDTERM EXAMINATION

PRACTICE QUESTIONS

 

Chapter 6: Continuous Distributions

1. Suppose that the time interval between arrivals of busses to a particular stop is a random variable X (in hours) with exponential distribution and parameter q=30.

  1. You arrive, panting, to the stop just after a bus leaves. What is the probability that you have to wait at most 15 minutes for the next bus?

  2. Suppose that the next bus has not arrived 15 minutes later when a second person comes along. What is the probability that the newcomer will have to wait at least 15 more minutes?

2. Suppose that X has a uniform distribution with parameters a and 2a. What is the probability that it will take a value less than 3a/2.

3. Suppose that the number of days X between successive calls to a 24-hour "suicide hotline" has an exponential distribution with q=2.

  1. Find the probability that more than 2 days elapse between the calls.

  2. Suppose that this hotline did not receive any call for 2 days. What is the probability that they will not receive any call for 2 more days?

4. Suppose that X has an exponential distribution with parameter q. Find the probability that it will take a value less than -qln(0.9).

5. Suppose that the average calculus GPA (X) at a university is normally distributed with mean 2.2, and 95% of the time, the GPA is between 1.6 and 2.8. Find the standard deviation of X.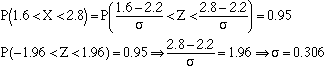

 

6. A random variable has a normal distribution with s=10. If the probability that the random variable will take on a value less than 82.5 is 0.8212, what is the probability that it will take a value greater than 58.3?

(HINT: Find the mean m first.)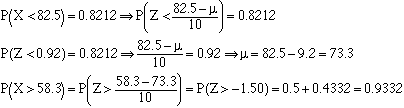

7. Suppose that X has a Normal distribution with mean 40. For what value of sigma is

P(20¾X¾60)=0.50.

 

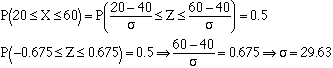
8. The personnel department of a large corporation gives two aptitude tests to job applicants. One measures verbal ability; the other, qualitative ability. From many year’s experience, the company has found that a person’s verbal score, Y1, is normally distributed with mean 50 and standard deviation 10. The quantitative scores, Y2, are normally distributed with mean 100 and standard deviation 20, and Y1 and Y2 appear to be independent. A composite score is assigned to each applicant, where

Y=3Y1+2Y2.

To avoid unnecessary paperwork, the company automatically rejects any applicant whose composite score is below 375. What is the chance that an applicant will fail the screening test?

 

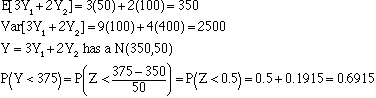
Chapter 8 (Sampling Distribution of the Mean)

1. A random sample of size 64 is taken from a normal distribution with m=51.4 and s=6.8. What is the probability that the mean of the sample will exceed 52.9?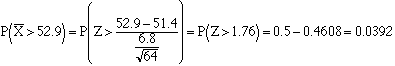

2. A random sample of size n=225 is to be taken from an exponential distribution with q=4.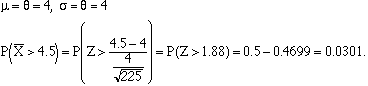

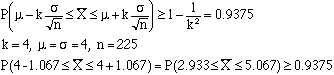
  1. Based on the central limit theorem, what is the probability that the mean of the sample, , will exceed 4.5?

  2. By using the Chebyshev’s theorem find c and d such that

 

3. A random sample of size 100 is taken from a normal distribution with m=12 and s=6. What is the probability that the mean of the sample will fall between 7 and 17?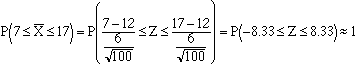

 

Chapter 8: Chi-Square, t, F distribution

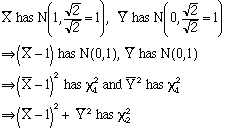
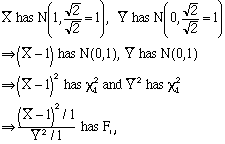
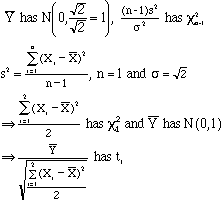
1. Let be a sample from an , and be an independent sample from an distribution.

    1. What is the distribution of ? Justify your answer.

    2. What is the distribution of ? Justify your answer.

    3. What is the distribution of
? Justify your answer.

d. Find .

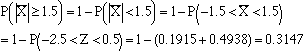
2. Suppose that X1 has a Normal distribution with m1=2 s12=9, X2 has a Normal distribution with m2=1 s22=4, and X3 has a Normal distribution with m3=3 s32=25 . Assume that X1 , X2 and X3 are independent.

What is the distribution of ?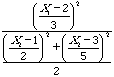

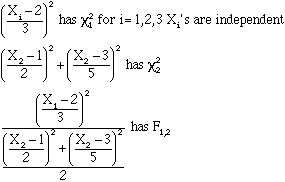
TABLE USE PROBLEMS:

3. If and are the variances of independent random samples of size and from a standard normal distribution, find

a.

b.

Order Statistics

1. Find the sampling distribution of smallest and largest order statistics (Y1 and Yn) for a sample of size n from a population having an exponential distribution with q. Find the mean and variance of the smallest order statistics. (HINT. Look at the functional form of pdf and compare it with the well known distributions.)