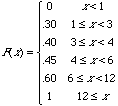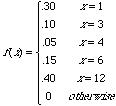
INTRODUCTION TO MATHEMATICAL STATISTICS

SOLUTIONS TO THE SECOND MIDTERM EXAMINATION

1. An insurance company offers its policyholders a number of different premium payment options. For a randomly selected policyholder, let X=the number of months between successive payments. The d istribution function (cumulative distribution function) of X is as follows:

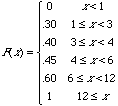e. pdf of X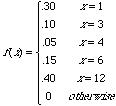

  1. Find P(X=4)=.45-.40=.05

  2. Find P(3_X_6)=.60-.30=.30

  3. Find P(1<X<5)=.45-.30=.15

  4. Find P(X>4)=1-.45=.55

2. Suppose E(X)=5 and E[X(X-1)]=27.5. E[X(X-1)]= E[X2]-E[X]= E[X2]-5=27.5

  1. Find E(X2) =32.5

  2. Find Var(X)=32.5-25=7.5

3. Let X denote the amount of time for which a book on 2-hour reserve at a college library is checked out by a randomly selected student and suppose that X has a probability density function

  1. Find the value of k.

  2. Find P(.5_X_1.5) =

  3. Find the distribution function of X.

  4. Find the expected value of X.

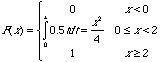
4. Let X,Y have a joint probability density function

  1. Find the marginal distribution of X

  2. Find the conditional distribution of Y given X=.5

5. A service station has both self-service and full-service islands. On each island, there is a single regular unleaded pump with two hoses. Let X denote the number of hoses being used on the self-service island at a particular t ime, and let Y denote the number of hoses on the full service island in use at that time. The joint probability distribution of X and Y appears in the accompanying tabulation.

 

x

0

1

2

y

0

.10

.04

.02

1

.08

.20

.06

2

.06

.14

.30

  1. What is P(X=1 and Y=1)?.20

  2. Compute P(X_1,Y_1)=.10+.04+.08+.20=.42

  3. Find P(X=Y)=f(0,0)+f(1,1)+f(2,2)=.60

  4. Find P(X+Y_2)=.1+.04+.02+.08+.06+.2=.50

  5. Are the X and Y independent?f(0,0)=.10, but g(0)h(0)=.24(.16)=.0384 (not independent

6. The moment generating function for a random variable X is .

  1. Find E[X].
  2. Find the standard deviation of X.
  3. Find the moment generating function of Y=1-X.

7. A study of the nutritional value of a certain kind of bread shows that the amount of thiamine (vitamine B1) in a slice of bread may be looked upon as random variable with m=0.260 milligram and s=0.005 milligram.

  1. According to the Chebyshev's theorem what probability can we assert for P(0.24<X<0.28).
  2. According to the Chebyshev's theorem, between what values must be the thiamine content of at least 35/36 of all slices of this bread?