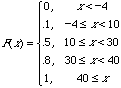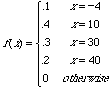INTRODUCTION TO MATHEMATICAL STATISTICS MATH. 2611
SOLUTIONS TO THE FIRST MIDTERM EXAMINATION
SPRING, 20011.
where certain dots were raised, the choice depending on the character being transcribed. The letter e, for example, has two raised dots and is written
Punctuation marks, common words, suffixes, and so on also have specified dot patterns. In all how many different characters can be enciphered in Braille? 
B. A computer is instructed to generate a random sequence of size 11 using the digits 0 through 9; repetitions are permissible. What is the probability that such a sequence will have at least one 4?
C. Does a monkey have a better chance of rearranging ACCLLUUS to spell CALCULUS or AABEGLR to spell ALGEBRA?
Please justify your answer.
For the first one there are
distinguishable outcomes. For the second one there are 
distinguishable outcomes. Therefore writing ALBEBRA is more likely.
D. Eight politicians meet at a fund-raising dinner. How many greetings can be exchanged if each politician shakes hands with every other politician exactly once? 
2. A.
Find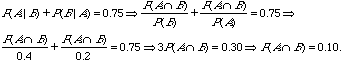
if 
, 
, and 
.
B. Suppose that P(A)=0.4, P(B)=0.5, and 
. Find the Probability 
.
3. Two proofreaders are responsible for finding punctuation errors in the editorial section of a newspaper. A : Jim has an 50% chance of spotting a hyphenation error, while B: Sally picks up on that same kind of mistake 80% of the time. If the probability is 0.40 that both will see a problem, what is the probability that a hyphenation error will go undetected? Are the events that Jim and Sally recognize a given error independent?
4. Suppose that two fair dice (one red and one green) are thrown, with events A, B, and C defined as follows:
A: a 1 or a 2 shows on the red die B: a 3, 4, or 5 shows on the green die C: the dice total is 4, 11, or 12
YES
NO
. 
|
Red die |
||||||
|
Green die |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
(1,5) |
(1,6) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
(2,5) |
(2,6) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
(3,5) |
(3,6) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
(4,5) |
(4,6) |
|
5 |
(5,1) |
(5,2) |
(5,3) |
(5,4) |
(5,5) |
(5,6) |
|
6 |
(6,1) |
(6,2) |
(6,3) |
(6,4) |
(6,5) |
(6,6) |
5.
Brett and Margo have each thought about murdering their rich Uncle Basil in hopes of claiming their inheritance a bit early. Hoping to take advantage of Basil's predilection for immoderate desserts, Brett has put rat poison in the cherries flambé; Margo, unaware of Brett's activities, has laced the chocolate mousse with cyanide. Given the amounts likely to be eaten, the probability of the rat poison being fatal(F) is 0.75; the cyanide, 0.90. Based on other dinners where Basil was presented with the same dessert options, we can assume that he has a 50% chance of asking for the cherries flambé(A), a 40% chance of ordering the chocolate mousse(B), and a 10% chance of skipping dessert altogether(C). No sooner are the dishes cleared away when basil drops dead.6. A criminal judge has heard many cases where the defendant was charged with grand theft auto and the jury returned a guilty verdict. But the final disposition was not always the same. Mitigating circumstances of various kinds led the judge over the years to impose unequal jail terms for what was basically the same offense. Looking back over court transcripts, s/he sees that x, the imposed sentence length (in years) has a distribution that can be described quite well by a continuous probability density function having the form
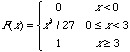
7. If the cumulative distribution function (df) of a random variable X, F, is given by
