This statlet performs an analysis of variance for data grouped by levels of a single classification factor, where the data are grouped into blocks according to a blocking factor. The tabs are:
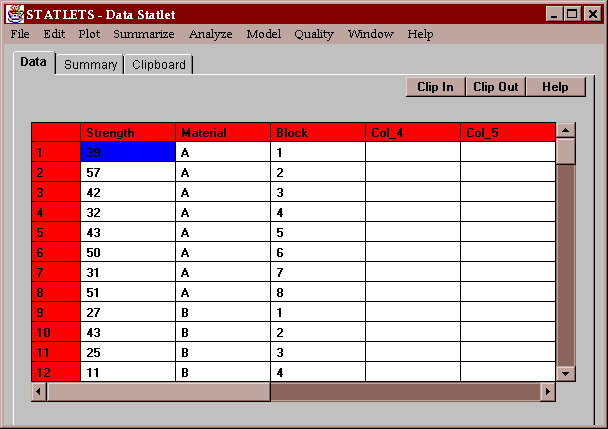
The example data consists of the measured breaking strength of 32 widgets. 8 widgets were made from each of 4 materials, divided into 8 blocks. The resulting strengths are shown below:

The Randomized Block Design statlet performs a similar analysis to this statlet, where the data for each material are placed into separate columns and the rows define the blocks.
Enter the name of the column containing the measurements, the name of the column containing the level codes for the experimental factor, and the name of the column containing the level code for the blocks:
This tab shows a plot of the data values by level code:
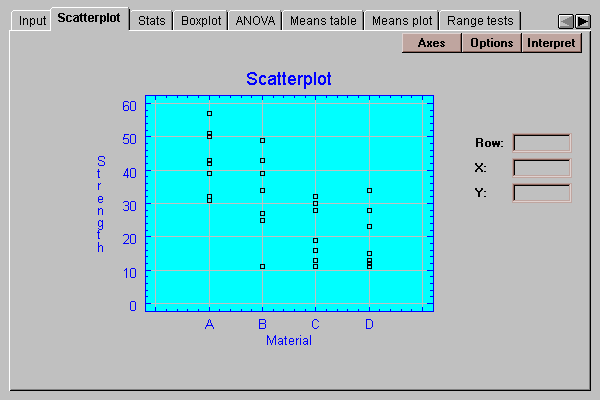
Notice that the strengths of the widgets made from materials A and B appear to be greater than that of widgets made from materials C and D.
Specify the desired orientation for the plot:

Indicate the axis along which the data values will be displayed.
This tab displays a table of summary statistics for each level code:
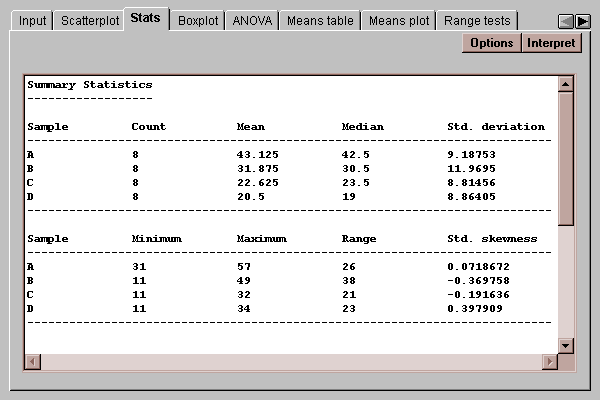
Initially, a set of commonly computed statistics is displayed. You can request other statistics by pressing the Options button.
For a discussion of other summary statistics, refer to the One Variable Analysis statlet.
The Options button permits you to select any of 18 different statistics to compute:
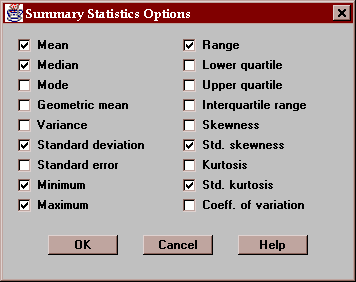
For definitions of each of these statistics, refer to the Glossary.
This tab displays box-and-whisker plots by level code:
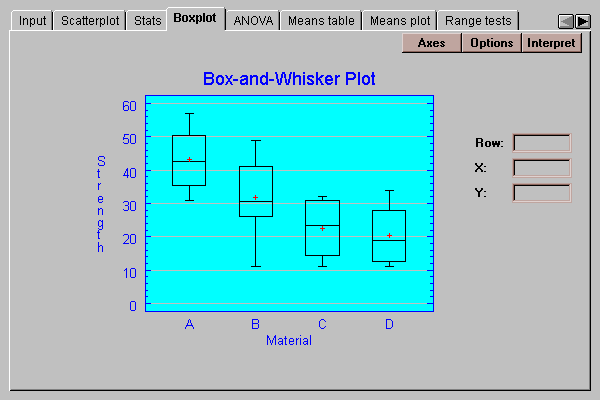
Box-and-whisker plots are useful graphs for displaying many aspects of samples of numeric data. Their construction is discussed in the One Variable Analysis statlet.
The Options button permits you to control various aspects of the plot:
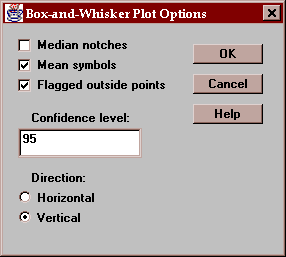
These include:
Median notches - if checked, notches are added to the boxes indicating the location of uncertainty intervals for the medians. These intervals are scaled in such a way that if two intervals do not overlap, there is a statistically significant difference between the two population medians at the indicated confidence level.
Mean symbols - if checked, the location of the sample means are shown as plus signs.
Flagged outside points - if checked, the whiskers extend outward to the most extreme points which are not outside points. All outside points are marked with special symbols. If not checked, the whiskers extend outward to the minimum and maximum values in the samples.
Confidence level - specifies the confidence level for the median notches.
Direction - specifies the orientation of the plot.
This tab displays an analysis of variance table for the data:
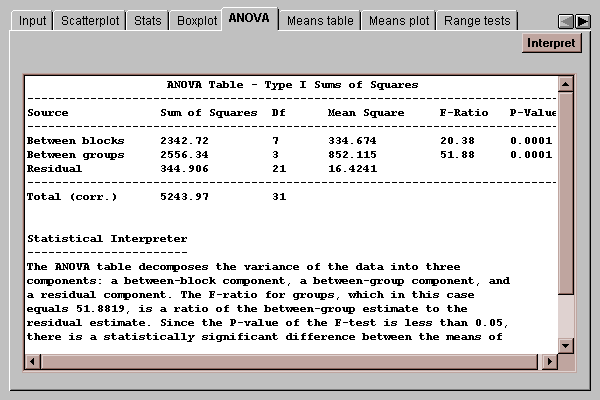
The table takes the original variability among the 32 measured breaking strengths and divides it into three components:
The P-values in the rightmost column of the table are used to determine whether significant differences exist between rows and between columns. P-values below 0.05 indicate statistically significant differences at the 5% significance level. In the above example, there are significant differences between both rows and columns.
This tab displays the means for each level code together with uncertainty intervals:
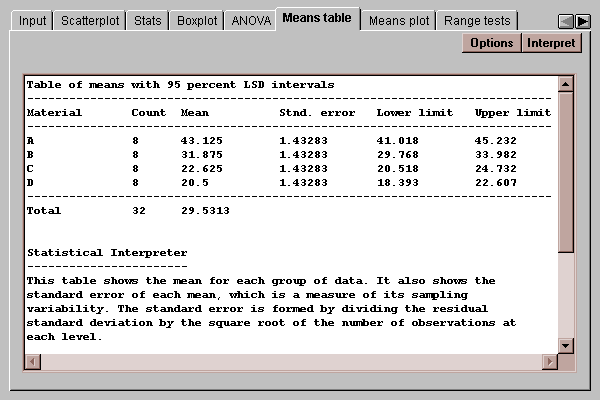
The uncertainty intervals bound the estimation error in the means using one of several methods, selected by pressing the Options button. The choice of intervals is described in detail in the Oneway ANOVA statlet.
Select the desired type of uncertainty intervals:
This tab plots the level means with uncertainty intervals:
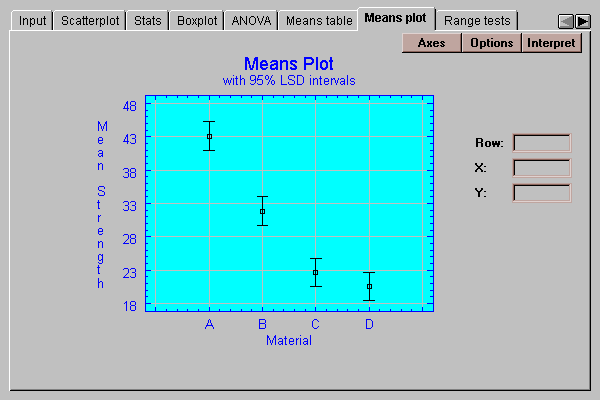
See the discussion under Means table for an explanation of the intervals.
Select the desired type of uncertainty intervals:

This tab indicates which means are significantly different from which others:
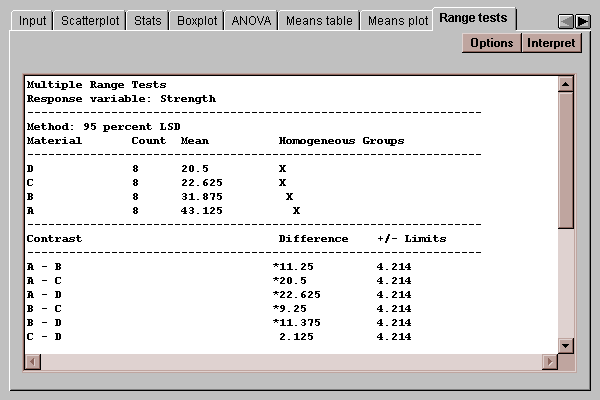
The output of this tab is described in the Oneway ANOVA statlet.
Select the desired procedure and the level of confidence:
This tab plots the residuals by level code:
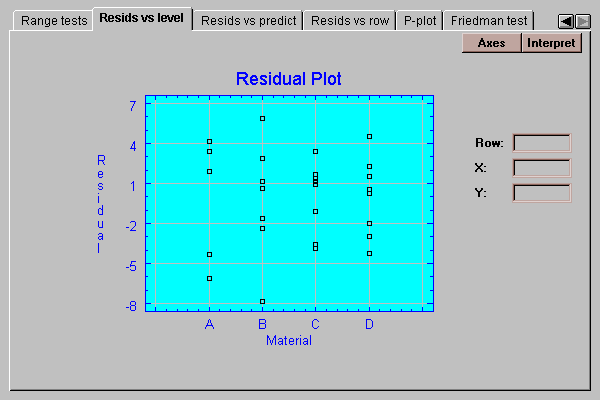
If the standard deviations within each group are the same, we should see approximately the same scatter amongst the residuals for each material. In this case, there are small differences between the spreads of the residuals in the four groups. We don’t usually start to worry, however, until the standard deviations differ by more than a factor of 3 to 1 between the largest and the smallest. The analysis of variance is known to be reasonably robust at differences of less than this magnitude, which means that the confidence levels stated are approximately correct. The differences here are much less than 3 to 1.
This tab plots the residuals versus predicted values of strength:
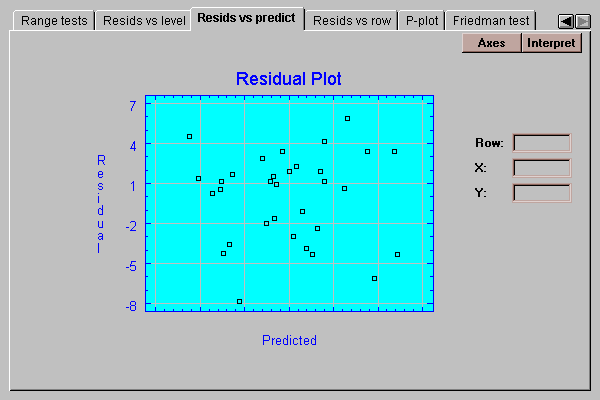
It is useful for detecting possible violations of the assumption of constant within group variability. Frequently, the variability of measurements increases with their mean. If so, the above plot would show points falling into a funnel-shaped pattern, increasing in spread from left to right. Such observed heteroscedasticity may often be eliminated by analyzing the logarithms of the data rather than the original data values.
This tab plots the residuals versus row number:
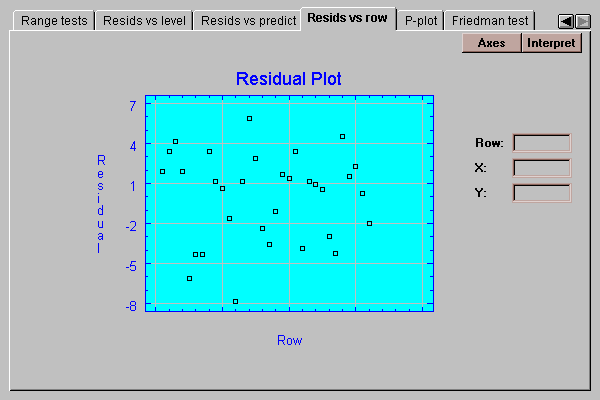
If the data were entered in time order, any pattern in the above plot would indicate changes over the course of the data collection.
This tab creates a normal probability plot for the residuals:
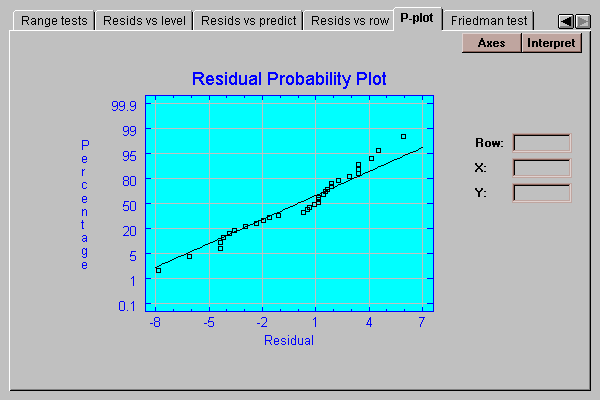
If the residuals come from a normal distribution, the points should lie approximately along a straight line as shown above.
This tab displays the results of a Friedman rank sum test:
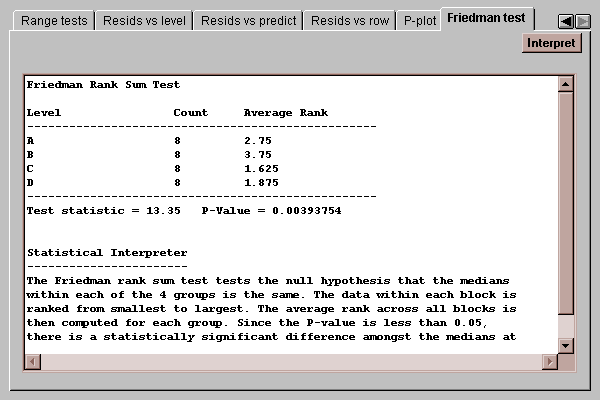
This test is a nonparametric alternative to the standard analysis of variance. It tests the hypotheses:
H0: all group medians are equal
HA: all group medians are not equal
A P-value below 0.05, as in the above table, indicates a statistically significant difference between the medians at the 5% significance level.