This statlet compares samples taken from several different populations. It calculates summary statistics, performs an analysis of variance, and displays the data in various ways. The tabs are:
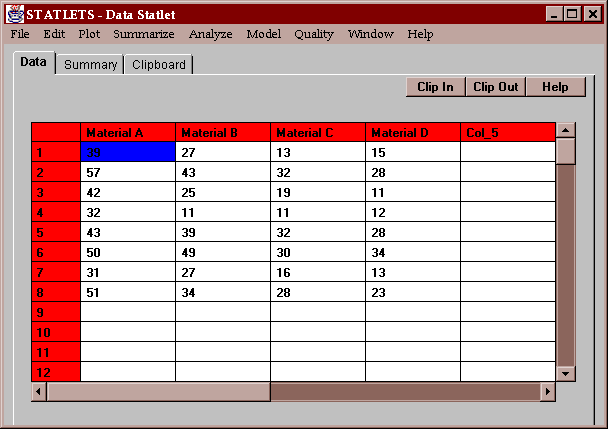
The example data consists of the measured breaking strength of 32 widgets. 8 widgets were made from each of 4 materials, and the resulting strengths are shown below:

The Oneway ANOVA statlet performs a similar analysis to this statlet, with all measurements placed into a single column and a second column indicating the type of material.
Enter the names of the columns containing each of the data samples:
All columns must contain numeric data. The numbers of observations in the columns may be different.
This tab shows a plot of the data values by column:
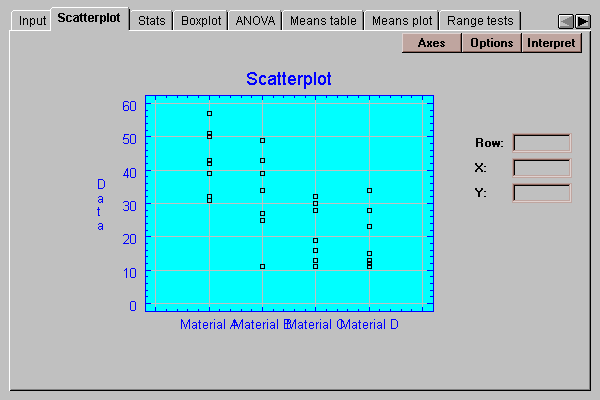
Notice that the strengths of the widgets made from materials A and B appear to be greater than that of widgets made form materials C and D.
Specify the desired orientation for the plot:

Indicate the axis along which the data values will be displayed.
This tab displays a table of summary statistics for each column:
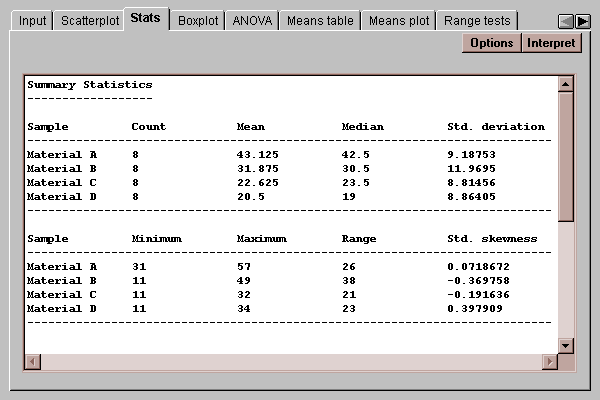
Initially, a set of commonly computed statistics is displayed. You can request other statistics by pressing the Options button.
For a discussion of other summary statistics, refer to the One Variable Analysis statlet.
The Options button permits you to select any of 18 different statistics to compute:
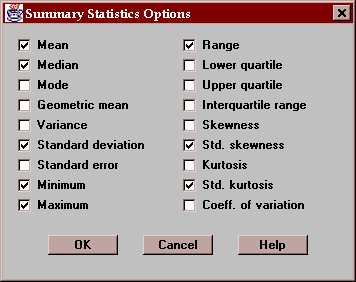
For definitions of each of these statistics, refer to the Glossary.
This tab displays box-and-whisker plots for the different samples:
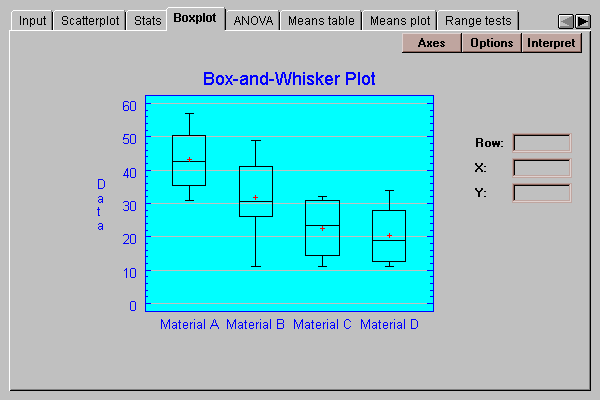
Box-and-whisker plots are useful graphs for displaying many aspects of samples of numeric data. Their construction is discussed in the One Variable Analysis statlet.
The Options button permits you to control various aspects of the plot:
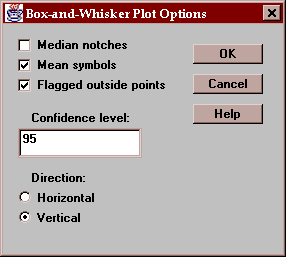
These include:
Median notches - if checked, notches are added to the boxes indicating the location of uncertainty intervals for the medians. These intervals are scaled in such a way that if two intervals do not overlap, there is a statistically significant difference between the two population medians at the indicated confidence level.
Mean symbols - if checked, the location of the sample means are shown as plus signs.
Flagged outside points - if checked, the whiskers extend outward to the most extreme points which are not outside points. All outside points are marked with special symbols. If not checked, the whiskers extend outward to the minimum and maximum values in the samples.
Confidence level - specifies the confidence level for the median notches.
Direction - specifies the orientation of the plot.
The plot below includes median notches drawn at the 95% confidence level:
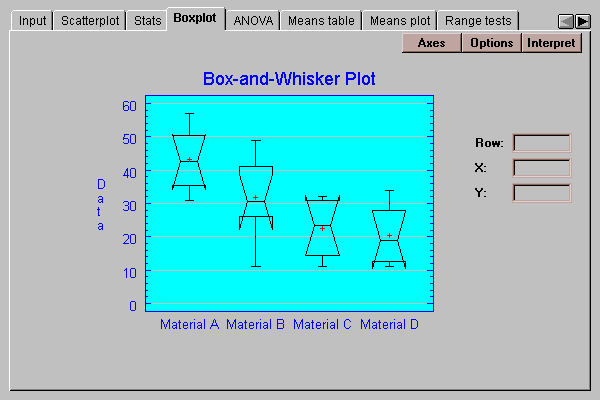
Since the notch for material A overlaps the notch for material B, those two medians are not significantly different from each other at the 95% confidence level. However, the notch for material A does not overlap the notches for materials C and D, making the median of A significantly different than the medians of C and D.
This tab displays an analysis of variance table for the data:
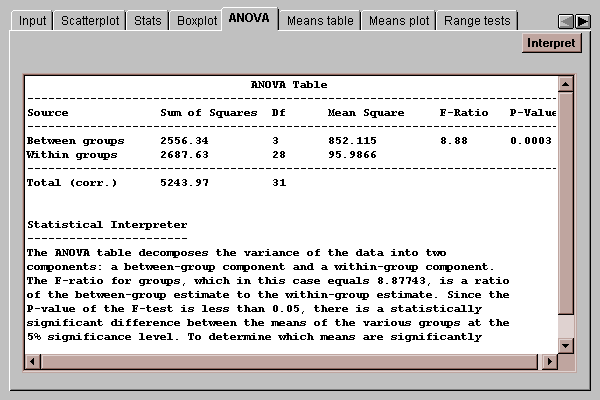
The table takes the original variability among the 32 measured breaking strengths and divides it into two components:
Obviously, the between group estimate shown above is much larger than the within group estimate, suggesting that there are real differences between the means. The statistical question is whether the second estimate is enough larger than the first estimate to reject the idea that the means are the same with at least 95% confidence. A formal hypothesis test can be formulated of the form:
H0: mu1 = mu2 = mu3 = mu4
HA: not all means equal
The statistic used to test these hypotheses is the F-ratio given by
F = between group mean square / within group mean square
If F is sufficiently large, we reject the null hypothesis that all the means are equal. In this case, F=8.88. Since the P-value of 0.0003 is well below 0.01, we can reject the null hypothesis and state that there are significant differences between the four group means at the 1% significance level. This does not imply that all the means are different from all the others. It simply implies that they are not all the same. To determine which means are significantly different from which others, use the Range tests tab described below.
This tab displays the mean of each group together with uncertainty intervals:
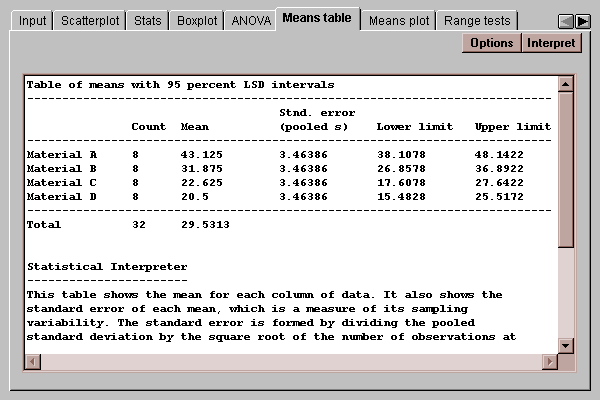
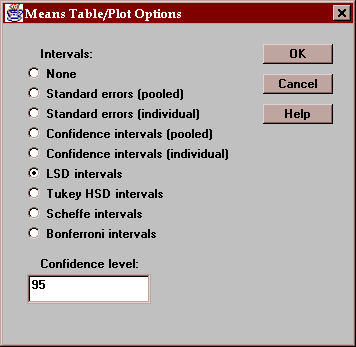
The uncertainty intervals bound the estimation error in the means using one of several methods, selected by pressing the Options button. The choice of intervals is:
None - no intervals are displayed.
Standard errors (pooled) - the interval is
xbar +/- sigmap/ni0.5
Standard errors (individual) - the interval is
xbar +/- sigmai/ni0.5
Confidence intervals (pooled) - the interval is
xbar +/- tn-k,alpha/2sigmap/ni0.5
Confidence intervals (individual) - the interval is
xbar +/- tni-1,alpha/2sigmai/ni0.5
LSD intervals - the interval is
xbar +/- tn-k,alpha/2sigmap/(2ni)0.5
Tukey HSD intervals - the interval is
xbar +/- Tn,k,alphasigmap/ni0.5
Scheffe intervals - the interval is
xbar +/- [(k-1)Fk-1,n-k,alpha]0.5sigmap/(2ni)0.5
Bonferroni intervals - the interval is
xbar +/- tn-k,alpha/[k*(k-1)]sigmap/(2ni) 0.5
where sigmai is the standard deviation of the i-th group, sigmap is the pooled standard deviation amongst the groups, n is the total number of observations, k equals the number of groups, t is a value from Student's t distribution, T is a value from Tukey's T distribution, F is a value from Snedecor's F distribution, and alpha equals the probability of a Type I error.
The default intervals use Fisher's LSD procedure. Provided all of the group sizes are the same, we can determine which means are significantly different from which others using the LSD procedure by simply looking at whether or not a pair of intervals overlap in the vertical direction. Pairs of intervals which do not overlap indicate a statistically significant difference between the means at the 95% confidence level. If the group sizes are different, this procedure will be approximately correct.
The Tukey, Bonferroni, and Scheffe intervals are designed to control the experiment-wide confidence level, as discussed under Range tests.
Select the desired type of uncertainty intervals:
This tab plots the group means with uncertainty intervals:
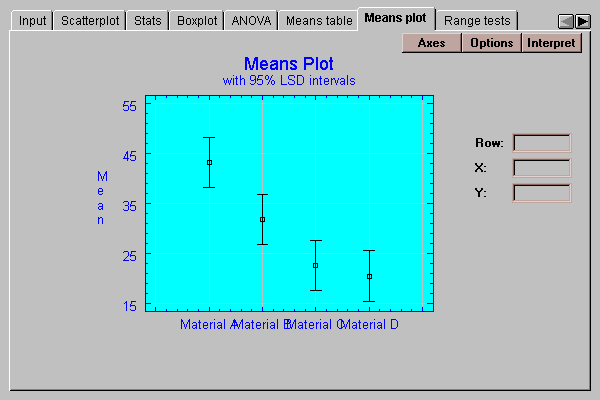
See the discussion under Means table for an explanation of the intervals.
Select the desired type of uncertainty intervals:

This tab indicates which means are significantly different from which others:
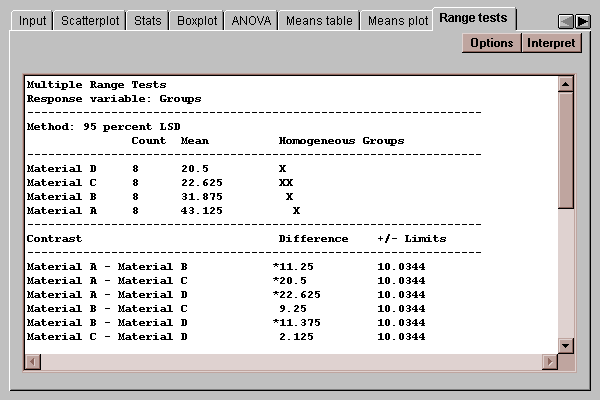
The top of this panel shows the four means, listed in increasing order of magnitude. The bottom part of the pane shows the difference between each pair of means, together with an interval of the form
difference +/- tn-k,alpha/2[MSE*(1/ni + 1/nj)]1/2
where ni and nj are the sizes of the two groups being compared, MSE is the mean squared error as shown in the ANOVA table, and tn-k,alpha/2 is a value from Student’s t distribution with n-k degrees of freedom leaving an area of alpha/2 in the upper tail of the curve (alpha is the probability of a Type I error, here set at 0.05). This interval amounts to a 95% confidence interval for the difference between the two means. If the interval covers 0, we cannot reject the idea that the two means may be equal at the 95% confidence level. The output places an asterisk next to each pair of means for which the interval does not contain 0, labeling these differences as statistically significant.
Also shown at the top right is an indication of homogenous groups, which are groups of means within which there are no statistically significant differences. In this case, materials C and D form one group, since they are not significantly different. Materials B and C form a second group, while material A stands by itself in a third group. The proper interpretation of this pattern is that material A is significantly stronger than all of the other materials. Material B is significantly stronger than material D but not than material C, while material C is not significantly different than either B or D. This apparent contradiction is clarified by noting that lack of a significant difference does not prove that two means are the same, it simply states that there is insufficient evidence to quantify the difference if it exists. In this case, we need more information about material C to discover which group it belongs to.
The Options button allows you to select the type of multiple comparison procedure to be applied. Fisher’s LSD procedure is only one of seven choices available for comparing pairs of means. Since each pairwise comparison in Fisher’s procedure has a 5% chance of being incorrect, one or more intervals may be incorrect as much as 30% of the time if you make six comparisons amongst the four groups. The other methods control the family error rate at 5%, i.e., insure that none of the differences will be declared significant when they shouldn’t be in more than 5% of the experiments we look at. In a oneway analysis of variance with equal group sizes, the most popular alternative to Fisher’s procedure is Tukey’s HSD (Honestly Significant Difference) procedure. Other procedures are available, including Dunnett's procedure which specifies one group as a control group and compares all other group means to the control mean.
Select the desired procedure and the level of confidence:
One important assumption underlying an analysis of variance is that the standard deviations within each group are the same. This is important because procedures such as the Range tests pool the standard deviations together to get a single estimate of the within group variance. This tab produces three statistics designed to test the assumption of equal group variances:
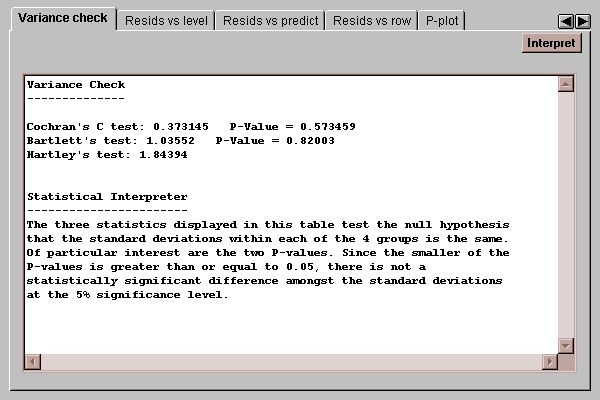
The statistics test the hypotheses:
H0: sigma1 = sigma2 = sigma3 = sigma4
HA: not all sigmas equal
Cochran’s test is computed by dividing the maximum group variance by the sum of the group variances. Bartlett’s test compares the geometric mean of the group variances to the arithmetic mean. Hartley’s test computes the ratio of the maximum group variance to the minimum group variance. The first two tests have P-Values associated with them. If a P-Value falls below 0.05, we can reject the hypothesis that the group sigmas are all the same at the 5% significance level. Hartley’s test result must be compared to a table of critical values found in various textbooks. In this case, neither P-Value is statistically significant, indicating that the difference in variability observed amongst the four groups is well within the range of normal sampling variability for groups of this size.
This tab plots the residuals by group:
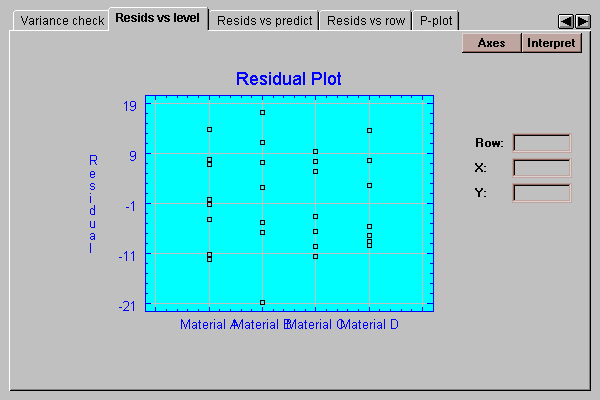
In a oneway analysis of variance, the residuals are equal to the data values minus the mean of the group from which they come. If the standard deviations within each group are the same, we should see approximately the same scatter amongst the residuals for each material. In this case, there are small differences between the spreads of the residuals in the four groups. We don’t usually start to worry, however, until the standard deviations differ by more than a factor of 3 to 1 between the largest and the smallest. The analysis of variance is known to be reasonably robust at differences of less than this magnitude, which means that the confidence levels stated are approximately correct. The differences here are much less than 3 to 1.
This tab plots the residuals versus predicted values of strength:
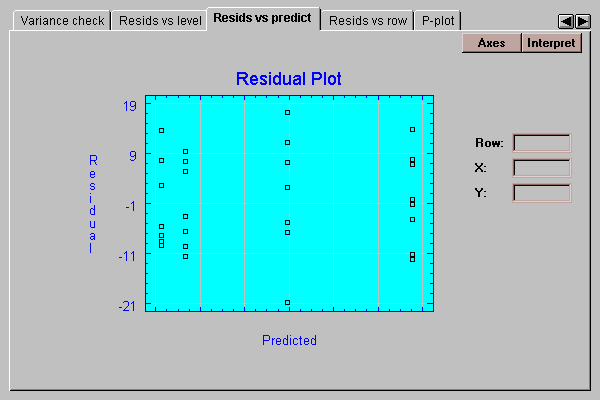
It is useful for detecting possible violations of the assumption of constant within group variability. Frequently, the variability of measurements increases with their mean. If so, the above plot would show points falling into a funnel-shaped pattern, increasing in spread from left to right. Such observed heteroscedasticity may often be eliminated by analyzing the logarithms of the data rather than the original data values.
This tab plots the residuals versus row number:
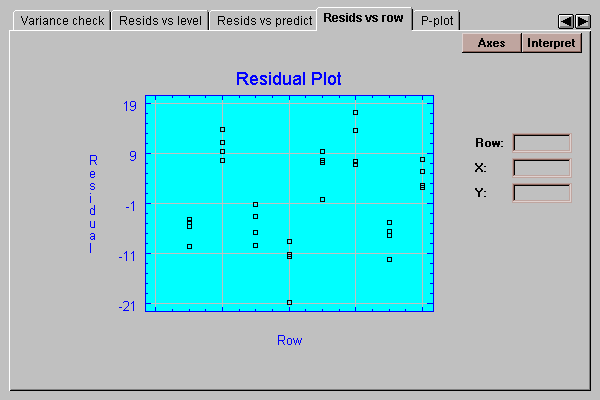
If the data were entered in time order, any pattern in the above plot would indicate changes over the course of the data collection.
This tab creates a normal probability plot for the residuals:
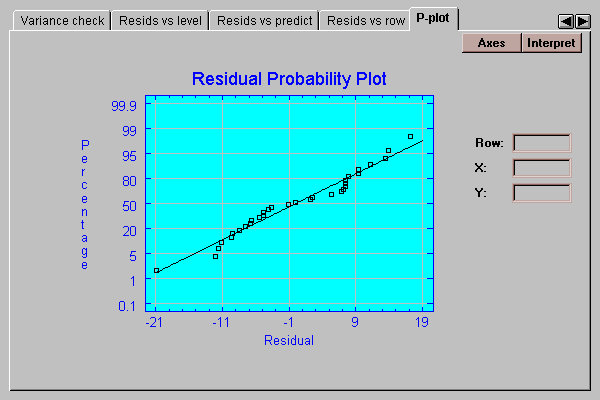
If the residuals come from a normal distribution, the points should lie approximately along a straight line as shown above.
An alternative to the standard analysis of variance (which compares the means of several groups) is the Kruskal-Wallis test. The Kruskal-Wallis test compares group medians, testing the hypotheses:
H0: all group medians are equal
HA: all group medians are not equal
The test begins by ranking all of the data values from smallest to largest, assigning a rank of 1 to the smallest and n to the largest. The average ranks of each group are then computed and compared to see if they differ by more than would be expected if the data in each group came from the same population. By using ranks, the impact of any outliers or skewness in the data is greatly diminished, allowing for a test which is not dependent on the data coming from a normal distribution.
This tab displays the results of the test:
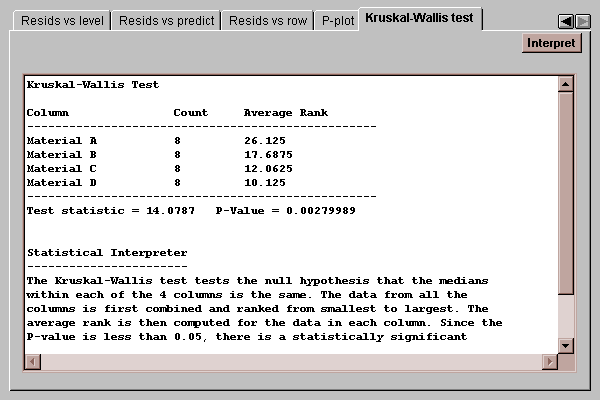
The average rank of the eight values in each group is shown, together with a test statistic and P-Value. If the P-value falls below 0.05 as in this case, we can reject the hypothesis that all of the medians are the same at the 5% significance level.
To determine which medians are significantly different from which others, select the Boxplot tab and use the Options button to ask for median notches.