|
|
![]()
|
STAT/MATH 2501 |
|
|
FALL, 2010 |
|
|
COURSE WEB SITE |
|
|
# OF CREDITS : |
4 |
|
PREREQUISITE: |
MATH.
1101 OR # |
|
DAYS & TIME: |
2:15-3:20
MWF |
|
BUILDING & ROOM: |
Sci.
3610 & 3550 |
|
INSTRUCTOR: |
Dr. Engin A. Sungur |
|
OFFICE: |
1350 SCIENCE |
|
TELEPHONE: |
x6325 |
|
OFFICE HOURS: |
MTWThF, 11-Noon |
|
E-Mail |
sungurea@morris.umn.edu |
COURSE DESCRIPTION: The course will
concentrate on Probability Theory and Statistical Methods. Probability theory;
set theory, axiomatic foundations, conditional probability and independence, Bayes’s Rule, random variables. Transformations
and expectations; expected values, moments and moment generating functions.
Common families of distribution; discrete and continuous
distributions. Multiple random variables; joint and
marginal distributions, conditional distributions and independence, covariance
and correlation, multivariate distributions. Properties
of a random sample and central limit theorem. Markov chains, Poison
processes.
COURSE MATERIAL: Sheldon, M. R., Introduction to
Probability Models (tenth edition), Academic Press, 2010
COURSE
WEB SITE: The
site includes general information about the course, activities and links to the
other sites. Students are encouraged to visit the page regularly and make
suggestions to the instructor for improvement. Some course activities are
located at the UMN Moodle server. There are three ways to
access Moodle site:
1.
Via my portal: Go to myU
Portal at http://myu.umn.edu,
login with your Internet ID, and click on the My Courses tab to see the links
to the Moodle sites to which you already have access. Note that the
majority of users with UofM Guest IDs are not able to
use myU portal at the moment.
2.
Via Moodle
server: Go to http://moodle.umn.edu
and login there with either your Internet ID or Guest ID. Once logged in, you
will be able to see the links to your own sites and also will be able to browse
and self-enroll in other sites that are open for public access
3.
Via Course Map: Click on Course News and
Announcements and Moodle site.
4.
Via direct method: On your browser just go to the following site:
https://moodle.umn.edu/course/view.php?id=11871
EXAMINATIONS: Three midterm
examinations and a final exam will be given. Each examination (including the
final) will be closed books and notes. But, you will be allowed to use an
information sheet. Time table and procedure for the examinations is given
below:
|
EXAM
1 |
SEPTEMBER
22 (Wednesday) |
SCI.
3610 & 3550 |
2:15-3:20 |
|
EXAM
2 |
OCTOBER
22 (Friday) |
SCI.
3610 & 3550 |
2:15-3:20 |
|
EXAM
3 |
NOVEMBER
22 (Monday) |
SCI.
3610 & 3550 |
2:15-3:20 |
|
FINAL |
DECEMBER
14 (Tuesday) |
SCI. 3610 & 3550 |
4:00-6:00 pm |
HOMEWORKS:. Eight homeworks will be assigned. Homework assignments will be given that correspond to each chapter in the
text. Due dates will be posted for each assignment on the Moodle
course site. Late homework will be penalized 50% of the point value. Students need to
download the assignment MS Word template from the course website, type their
answers and insert related graphs. All homework assignments are expected to be completed
with a word processor in electronic form. The assignments should be uploaded in
Moodle course website. Email submissions to the
instructor will not be accepted. Solutions will be available on the course Moodle website.
COURSE GRADE: The weights of homeworks midterm
exams and final exam are given below. During the lectures, time
to time, questions will be asked. If a student answers one of these
questions she/he will get an extra credit (1-10 pts) which
will be added to the overall score.
|
HOMEWORKS & ONLINE QUIZES: |
15% |
|
EXAMS: |
60% |
|
FINAL EXAM: |
25% |
|
A |
A- |
B+ |
B |
B- |
C+ |
C |
C- |
D+ |
D |
F |
|
90-100 |
88-89 |
86-87 |
80-85 |
78-79 |
76-77 |
70-75 |
68-69 |
66-67 |
60-65 |
0-59 |
S 68-100 N 0-67

PIN: To view your progress
in the course you need a student PIN. To get your PIN please visit the course Moodle web-site,
click on the get your pin button, and follow the instructions.
EXAMINATION & HOMEWORK POLICY: Exams will cover the material discussed in the class and the
readings in the text. Before the exam, an information sheet will be provided.
This information sheet (worksheet)
will include (a) place and date of the examination, (b) the detailed topics
that will be covered in the examination, (c) the tools that students must bring
to the examination (such as statistical tables, calculators etc.). One day
before the exam, the topics that will be included in the exam will be reviewed, and important points that
should be remembered will be pointed out. Right after the examination, the
students will get the solutions. The
anticipated grading time of the exams is 1 day.
The students should plan on taking the exam on
the scheduled date. Illness (Health Service Excuse) or a Chancellor's excuse
will be honored as a reason for taking the exam at other than the scheduled
date. (Make-ups creates a data which is not
independent and identically distributed. As you will learn in this course, lack
of these properties creates a big problem on the inference based on such data).
GRADING POLICY: The
difficulty of the exams will be so arranged that there will be no need for the
"normalization" of the scores based on the Gaussian
Distribution (known as making a curve). Trends on the scores, attendance
to the lectures, class participation etc. will be considered on the
determination of the final grades.
PLEASE FEEL WELCOME TO SEE ME OUTSIDE OF THE CLASS, ANY
TIME, IF YOU HAVE QUESTIONS, PROBLEMS, OR COMMENTS PERTAINING THE COURSE WORK.
![]()
![]()
The organization of the
in-class activities are summarized in the following flowchart. The main
components of the organization structure are:
SUMMARIES AND OUTLINE: These two components, hopefully, will provide a
smooth transition between the topics and lectures. These will answer three
basic questions: Where have we been?, Where are we
going?, and What have we learned?
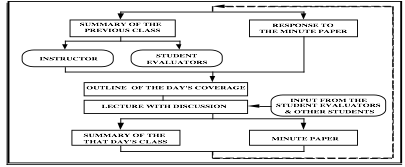
STUDENT EVALUATORS: Class participation and discussion
are very important on the learning process. Students are encouraged to ask
questions in the class. Questions, comments could help the instructor to set up
his/her pace. The input from the students should be constant. If you point out
the weaknesses of the instructor, and the problems with the course in general
as soon as possible your learning process will be enhanced. To formalize and
promote active learning, each in-class activity will be
evaluated by the two students. These students will be responsible to
point out all the problems that might affect the learning of the rest of the
class. For example, the topics that are not clearly covered,
pace of the lecture, use of the blackboard, problems with taking notes, etc. Time
to time student evaluators will be asked to make a summary of the
previous class.
|
EVALUATOR |
DATE 1 |
DATE 2 |
|
Armstrong,Douglas Erin |
8/25,27,30 |
10/4,6,8 |
|
Biessener,Fiona E |
9/1,3 |
10/11,13,15 |
|
Bitker,Guinevere Patrcia
Ellen |
9/8,10 |
10/20,22 |
|
Bruns,Kyle G |
9/13,15,17 |
10/25,27,29 |
|
Caswell,Amanda J |
9/20,22,24 |
11/1,3,5 |
|
Chen,Huan |
9/27,29,
10/1 |
11/8,10,12 |
|
Ding
Sr.,Liexiao |
10/4,6,8 |
11/15,17,19 |
|
Fragodt,Daniel |
10/11,13,15 |
11/22,23 |
|
Ginader,Timothy S |
10/20,22 |
11/29,
12/1,3 |
|
Harstad,Rachel K |
10/25,27,29 |
12/6,8,10 |
|
Jiao,Xueyang |
8/25,27,30 |
11/1,3,5 |
|
Orth,Jessica Marie |
9/1,3 |
11/8,10,12 |
|
Powers,Martin A |
8/25,27,30 |
11/15,17,19 |
|
Rach,Daniel M |
9/1,3 |
11/22,24 |
|
Riner,Alexander Thomas |
9/8,10 |
11/29,
12/1,3 |
|
Robinson,Casey Summers |
9/13,15,17 |
12/6,8,10 |
|
Taylor-Hempstead,Kelsey Ariel |
8/25,27,30 |
10/4,6,8 |
|
Thebault-Spieker,Jacob Charles |
9/1,3 |
10/11,13,15 |
|
Toffle,Nicholas R |
9/8,10 |
10/4,6,8 |
|
Vold,Elizabeth Marlo |
9/13,15,17 |
10/11,13,15 |
|
Wang,Gang |
9/20,22,24 |
10/20,22 |
|
Wang,Qianqian |
9/27,29, 10/1 |
10/25,27,29 |
|
Wang,Xuan |
10/4,6,8 |
11/1,3,5 |
|
Young,Ryan J |
10/11,13,15 |
11/8,10,12 |
|
|
10/20,22 |
11/15,17,19 |
|
|
8/25,27,30 |
11/22,23 |
|
|
9/1,3 |
11/29,
12/1,3 |
DISABILITIES
AND MENTAL HEALTH
As a student you may experience a range of issues
that can cause barriers to learning, such as strained relationships, increased
anxiety, alcohol/drug problems, feeling down, difficulty concentrating and/or
lack of motivation. These mental health concerns or stressful events may
lead to diminished academic performance or reduce your ability to participate
in daily activities. University of Minnesota services are available to
assist you with addressing these and other concerns you may be
experiencing. You can learn more about the broad range of confidential
mental health services available on campus via http://www.mentalhealth.umn.edu/
![]()
|
TOPIC |
TEXT BY ROSS |
ASSIGNMENTS |
STUDY GUIDE |
|
Introduction & Sample Space
and Events |
§ 1.1-1.2 |
Chapter 1 (pages
15-20) 1, 3, 4, 8, 17, 19, 23, 26, 30,
31, 36, 37, 39, 42, 44, 46 |
§ I.1-I.2 § I.3 |
|
Probabilities |
§ 1.3 |
§ I.4-I.5 |
|
|
Conditional Probabilities |
§ 1.4 |
§ I.5 |
|
|
Independent Events |
§ 1.5 |
§ I.5 |
|
|
Bayes' Formula |
§ 1.6 |
§ I.5 |
|
|
Random Variables |
§ 2.1 |
Chapter 2 Part I (pages
86-90) 1, 2, 3, 6, 7, 8, 10, 12, 13, 14,
20, 21, 27, 31, 33, 34, 35, 38 |
§ II.2-II.3 |
|
Discrete Random Variables |
§ 2.2 |
§ II.1 Discrete Mathematics, Binomial Theorem, Geometric Series, Maclaurin Series |
|
|
Continuous Random Variables |
§ 2.3 |
§ II.1 The Derivative of a
Function, Derivatives of the Composite Functions, The Definite Integral, Antidifferentiation, Evaluation of the Integrals, Methods
of Integration, Some Special Functions |
|
|
Expectation of a Random Variable |
§ 2.4 |
Chapter 2 Part II (pages
90-92) 39, 40, 43, 46, 47, 48, 50, 51 |
§ II.1 Evaluation of the Definite
Integrals by Using Antiderivatives, Methods of
Integration |
|
Jointly Distributed Random
Variables |
§ 2.5 |
Chapter 2 Part III (pages
92-95) 54, 55, 58, 60, 63, 68, 77 |
§ II.1 Some Results Involving
Multivariate Calculus |
|
Moment Generating Functions |
§ 2.6 |
§ II.1 Methods of Integration,
Some Results Involving Limits |
|
|
Limit Theorems |
§ 2.7 |
§ II.1 Some Results Involving
Limits |
|
|
Conditional Probability & Conditional Expectation |
Chapter 3 |
Chapter 3 (pages
173-181) 3, 4, 5, 7, 11, 13, 15, 35, 37, 46 |
§ II.1 |
|
Markov Chains |
Chapter 4 |
Chapter 4 (pages
275-279) 2, 3, 6, 7, 8, 10, 14, 20, 22, 29,
30 |
§ I.6 & II.1 |