What are they?

In most general terms, the purpose of the analyses via tree-building algorithms is to determine a set of if-then logical (split) conditions that permit accurate prediction or classification of cases. Classification tree (also known as decision tree) methods are a good choice when the data mining task is classification or prediction of outcomes and the goal is to generate rules that can be easily understood, explained, and translated into SQL (Structured Query Language) or a natural query language. Decision and regression trees are an example of a machine learning technique.

Classification tree labels records and assigns them to discrete classes. Classification tree can also provide the measure of confidence that the classification is correct.

CART builds classification and regression trees for predicting continuous dependent variables (regression) and categorical predictor variables (classification). The classic CART algorithm was popularized by Breiman et al. (Breiman, Friedman, Olshen, & Stone, 1984; see also Ripley, 1996). A general introduction to tree-classifiers, specifically to the QUEST (Quick, Unbiased, Efficient Statistical Trees) algorithm, is also presented in the context of the Classification Trees Analysis facilities, and much of the following discussion presents the same information, in only a slightly different context. Another, similar type of tree building algorithm is CHAID (Chi-square Automatic Interaction Detector; see Kass, 1980).

Advantages

• Simplicity of results. In most cases, the interpretation of results summarized in a tree is very simple. This simplicity is useful not only for purposes of rapid classification of new observations (it is much easier to evaluate just one or two logical conditions, than to compute classification scores for each possible group, or predicted values, based on all predictors and using possibly some complex nonlinear model equations), but can also often yield a much simpler "model" for explaining why observations are classified or predicted in a particular manner (e.g., when analyzing business problems, it is much easier to present a few simple if-then statements to management, than some elaborate equations).

• Tree methods are nonparametric and nonlinear. The final results of using tree methods for classification or regression can be summarized in a series of (usually few) logical if-then conditions (tree nodes). Therefore, there is no implicit assumption that the underlying relationships between the predictor variables and the dependent variable are linear, follow some specific non-linear link function [e.g., see Generalized Linear/Nonlinear Models (GLZ)], or that they are even monotonic in nature. For example, some continuous outcome variable of interest could be positively related to a variable Income if the income is less than some certain amount, but negatively related if it is more than that amount (i.e., the tree could reveal multiple splits based on the same variable Income, revealing such a non-monotonic relationship between the variables). Thus, tree methods are particularly well suited for data mining tasks, where there is often little a priori knowledge nor any coherent set of theories or predictions regarding which variables are related and how. In those types of data analyses, tree methods can often reveal simple relationships between just a few variables that could have easily gone unnoticed using other analytic techniques.

• Learning by induction (generalizing from examples) – but this does not guarantee the correct tree.

• Preselection of variables is not needed (a robust stepwise selection method is used).
  
• Invariant to monotonic predictor transformations, e.g. logarithmic transformations are not needed.
  
• Same variable can be reused in different parts of a tree, i.e. context dependency automatically recognized.
  
• Unlike a maximum likelihood method no single dominant data structure (e.g. normality) is assumed or required.
  
• Robust to the effects of outliers.
  
• Mixed data types can be used.

Overview

Classification tree is built through a process known as binary recursive partitioning. This is an iterative process of splitting the data into partitions, and then splitting it up further on each of the branches.

Initially, all objects are considered as a single group. the group is split into two subgroups using a creteria, say high values of a variable for one group and low values for the other. The two subgroups are then split using the values of a second variable. The splitting process continues until a suitable stopping point is reached. The values of the splitting variables can be ordered or unordered categories. It is this feature that makes the CART so general.

Examples

Suppose that the subjects are to be classified as heart-attack prone or non heart-attack prone on the basis of age, weight, and exrecise activity. In this case CART can be diagrammed as the following tree.

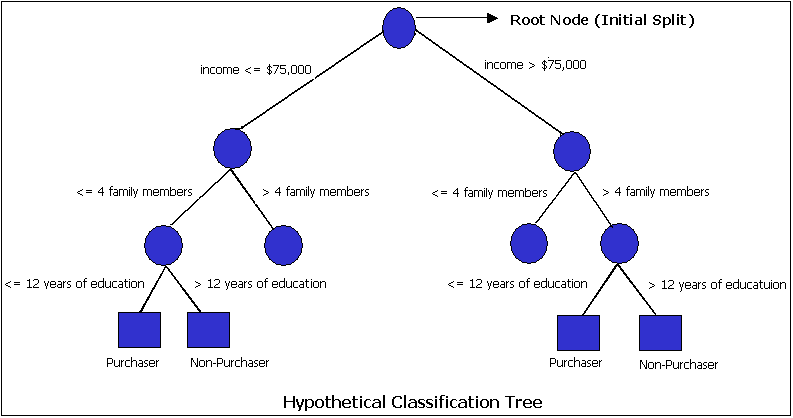
In this example the subjects are to be classified as puchaser or nonpurchaser based on their income, number of family members and years of education. You start with a training set in which the classification label (say, "purchaser" or "non-purchaser") is known (pre-classified) for each record.  All of the records in the training set are together in one big box. The algorithm then systematically tries breaking up the records into two parts, examining one variable at a time and splitting the records on the basis of a dividing line in that variable (say, income > $75,000 or income <= $75,000).  The object is to attain as homogeneous set of labels (say, "purchaser" or "non-purchaser") as possible in each partition.  This splitting or partitioning is then applied to each of the new partitions. The process continues until no more useful splits can be found. The heart of the algorithm is the rule that determines the initial split rule (see figure below).

Finding the initial split

The process starts with a training set consisting of pre-classified records. Pre-classified means that the target field, or dependent variable, has a known class or label ("purchaser" or "non-purchaser," for example). The goal is to build a tree that distinguishes among the classes. For simplicity, assume that there are only two target classes and that each split is binary partitioning. The splitting criterion easily generalizes to multiple classes, and any multi-way partitioning can be achieved through repeated binary splits. To choose the best splitter at a node, the algorithm considers each input field in turn.  In essence, each field is sorted. Then, every possible split is tried and considered, and the best split is the one which produces the largest decrease in diversity of the classification label within each partition (this is just another way of saying "the increase in homogeneity").  This is repeated for all fields,  and the winner is chosen as the best splitter for that node.  The process is continued at the next node and, in this manner, a full tree is generated.

Avoiding Overfitting: Pruning the tree 

Pruning is the process of removing leaves and branches to improve the performance of the decision tree when it moves from the training data (where the classification is known) to real-world applications (where the classification is unknown -- it is what you are trying to predict).  The tree-building algorithm makes the best split at the root node where there are the largest number of records and, hence, a lot of information. Each subsequent split has a smaller and less representative population with which to work.  Towards the end, idiosyncrasies of training records at a particular node display patterns that are peculiar only to those records. These patterns can become meaningless and sometimes harmful for prediction if you try to extend rules based on them to larger populations.

For example, say the classification tree is trying to predict height and it comes to a node containing one tall person named X and several other shorter people. It can decrease diversity at that node by a new rule saying "people named X are tall" and thus classify the training data.  In a wider universe this rule can become less than useless. (Note that, in practice, we do not include irrelevant fields like "name", this is just an illustration.)

Pruning methods solve this problem -- they let the tree grow to maximum size, then remove smaller branches that fail to generalize. 

Since the tree is grown from the training data set, when it has reached full structure it usually suffers from over-fitting (i.e. it is "explaining" random elements of the training data that are not likely to be features of the larger population of data). This results in poor performance on real life data. Therefore, it has to be pruned using the validation data set .