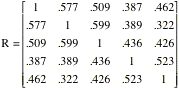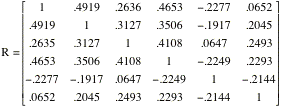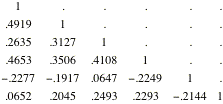STATISTICAL COMPUTING ACTIVITY: PRINCIPAL COMPONENT ANALYSIS FROM DATA

 

The data set that we will be using is the 1988 Olympic Decathlon, given in Table 2.2. Note that

Events: (1) 100m, (2) long jump, (3) shot putt, (4) high jump, (5) 400m, (6) 110m hurdles, (7) discus, (8) pole vault, (9) javelin, (10) 1500m.

 

Step 1. Download olympic.xls from the web site.

Step 2. Click on the file to open Excel

(We need to modify the data first. That is the reason why we are running Excel.)

Step 3. Highlight the last row and delete it by going Edit/Clear/All.

(Since this athlete is a suspected outlier.)

Step 4. Transform the data by taking negative values for the four running events, i.e., event1, event5, event6, event10.

(So that all events are scored in the same direction; small scores reflect poor performance, large scores reflect the good performance.)

Step 5. Save the file as modoly.xls and modoly.txt

 

Or

Step 1. Download modifiedolympic.txt from the web site.

Step 2. Run R

Step 3. Go to File menu and ³Change directory² to the location that you have saved the file

 

>modoly=read.table(³modifiedolympic.txt², header=T)

>attach(modoly)

 

To see the variable names and data type

 

> modoly

 

Let us do PCA by using correlation matrix

 

>prcomp(modoly, scale=T)

 

This will give you Table 3.3. Note that R gives you the standard deviations, Table 3.3 gives you the variances,

 

To save results, type

 

>modoly.pc=prcomp(modoly, scale=T)

 

Now try

 

>summary(modoly.pc)

 

To get a scree plot

 

>plot(modoly.pc)

 

To produce a biplot

 

>biplot(modoly.pc)

 

Or

 

>princomp(modoly, cor=TRUE)

 

>modoly.pc=princomp(modoly, cor=T)

>summary(modoly.pc, loadings=TRUE)

 

To get the scree plot

 

>screeplot(modoly.pc)

 

To produce a biplot

 

>biplot(modoly.pc)

 

>plot(modoly.pc$scores[,1],modoly.pc$[,2],xlab=²PC1²,ylab=²PC2²)

 

This is Figure 3.3. Note that the signs are arbitrary in PCA.

 

     STATISTICAL COMPUTING ACTIVITY: PRINCIPAL COMPONENT ANALYSIS FROM A GIVEN COVARIANCE OR CORRELATION MATRIX

 

First we need to learn how to enter a matrix

 

>example1=matrix(c(1,2,3,4,5,6), nrow=3, byrow=T)

 

To see the matrix

 

>example1

 

Now try

 

>example2=matrix(c(1,2,3,4,5,6), nrow=2, byrow=T)

>example2

 

Now enter the correlation matrix for the weekly rates of return for Allied Chemical, duPont, Union Carbide, Exxon, and Texaco.

 

 

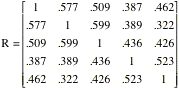
>return=matrix(c(1, .577, .509, Š , .523, 1), nrow=5, byrow=T)

>eigen(return)

 

STATISTICAL COMPUTING ACTIVITY: PRINCIPAL COMPONENT ANALYSIS FROM DATA

 

Step 1. Download olympic.xls from the web site.

Step 2. Run SYSTAT

 

File

            Open

                        Data

 

Change Files of Type to All Files (*.*)

Locate the folder that you have saved the file

Select the file

Click Open

 

Click on line 34

Edit

            Cut

 

To change the signs of event1, event5, event6, event10

 

Data

            Transform

                        =Let

Type negevent1 in the Variable box and -event1 in the Expression box

Repeat this for event5, event6, and event10

 

Analysis

            Multivariate Analysis

                        Factor Analysis

From Available variable(s) window select negevent1, event2, event3, event4, negevent5, negevent6, event7, event8, event9, negevent10 by double clicking on them

 

Make sure that Principal components (PCA) is selected as Method and Correlation is selected as Matrix for extraction

 

Get rid off 1 and type 0 in the Minimum eigenvalue window.

 

Check extended results

 

Click on Save tab

Select Factor scores

Check Save data with scores

Click on Š at the end of the Filename and select where you want to save the file

Type a file name, say olympicpca

Click OK

 

 

STATISTICAL COMPUTING ACTIVITY: PRINCIPAL COMPONENT ANALYSIS FROM A GIVEN COVARIANCE OR CORRELATION MATRIX

 

 

Over a period of five years, yearly samples of fishermen on 28 lakes in Minnesota were asked to report the time they spent fishing and how many of each type of gane fish they caught. Their responses were then converted to a catch rate per hour for

x1=Bluegill, x2=Black crappie, x3=Smallmouth bass, x4=Largemouth bass, x5=Walleye, x6=Northern pike.

 

Fish caught by the same fisherman live alongside of each other, so the data should provide some evidence on how the fish group. The first four fish belong to the centrarchids, the most plentiful family. The walleye is the most popular fish to eat.

 

Now let us carry out principal component analysis on this data

 

 

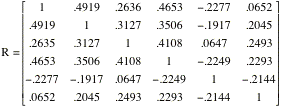
First we need to enter correlation matrix to SYSTAT

 

Utilities

            Matrix

                        Read

Give a name to your matrix, say fish

 

Since the matrix is symmetric it is enough to  enter diagonal and lower diagonal elements of the matrix remaining values will be entered as ³.²:

 

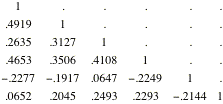
On the keyboard data window you enter the matrix like this

firstrow; secondrow; thirdrow Š (That is rows elements are separated with commas, rows separated with semi colons. Here it is:

 

1, ., ., ., ., .; .49919, 1, ., ., ., .; .2635, .3127, 1, ., ., .; .4653, .3506, .4108, 1, ., .; ŠŠ..

 

Check column names and type variable names on the window: say x1, x2, x3, x4, x5, x6

 

Check save matrix, by clicking on Š on the next window select the folder that you would like to save the file and type a name, say fishcor. Also select Correlation from the last window.

 

Click OK

 

Now we will load the file

Edit

            Open

                        Data

Locate the fishcor and double click.

 

Analysis

            Multivariate Analysis

                        Factor Analysis

Perform a PCA using only x1 through x4.

Perform a PCA using all six variables.

Interpret your results.