|
|
|
|
|
STAT. 1601 |
|
|
|
FALL
2010 |
|
|
|
COURSE
WEB SITE |
||
|
#
OF CREDITS : |
4 |
|
|
PREREQUISITE: |
High school higher algebra |
|
|
DAYS
& TIME: |
8:00-10:00 am |
|
|
BUILDING
& ROOM: |
SCI. 3610 & SCI. 3550 |
|
|
INSTRUCTOR: |
Dr.
Engin A. Sungur |
|
OFFICE: |
1350
SCIENCE |
|
TELEPHONE: |
x6325 |
|
OFFICE HOURS: |
Noon-1
pm |
|
E-Mail |
COURSE DESCRIPTION:
Scope,
nature, tools, language, and interpretation of elementary statistics.
Descriptive statistics; graphical and numerical representation of information;
measures of location, dispersion, position, and dependence; exploratory data
analysis. Elementary probability theory, discrete and continuous probability
models. Inferential statistics, point and interval estimation, tests of statistical
hypotheses. Inferences involving one or two populations, ANOVA, regression
analysis, and chi-square tests; use of statistical computer packages
(StatCrunch); community-based research/service learning.
GOALS OF
THE COURSE:
1. Learn to understand the main features
of traditional and modern statistics.
2. Learn how to analyze statistical data
properly.
3. Understand the role of formal
statistical theory and informal data analytic methods.
4. Gain an understanding of statistical
methods relevant to upper division interdisciplinary courses.
5. Sharpen students statistical intuition
and abstract reasoning as well as their reasoning from numerical data through
community-based and other research.
6. Enhance students’ critical thinking in
domains involving judgments based on data and stimulate the type of independent
thinking requiring research beyond the confines of the textbook, through
projects, interdisciplinary examples and exercises.
Our aim is to enable the students to appreciate the
richness of Statistical Science invite them to the probabilistic
thinking. Statistics is the science of the future. Any technique
that you are going to learn will help you to understand the unknown better,
and in turn it will increase in your success in other courses and in your
future professional career. We strongly encourage you to take the other
advanced level statistics courses.
We hope
that you will like statistics and choose it as a field that you would like to
work in and see the power of the statistics on enriching the quality of life of
the community that you are a part of.
COURSE MATERIAL:
MOORE,
S. D., and McCABE, G. P. , Introduction to the Practice of Statistics,
Sixth Edition, Freeman Press, 2009
COURSE WEB SITE:
Extensive lecture notes,
links, formula sheets, old exams, and other course materials are available on
the course open and Moodle websites. Instructions will be given in class
regarding access to these materials. The sites include general information about the
course, activities and links to the other sites related with the statistics.
Students are encouraged to visit the page regularly and make suggestions to the
instructor for improvement.
There are four ways to access Moodle site:
1.
Via my portal: Go to myU Portal at http://myu.umn.edu, login with your Internet
ID, and click on the My Courses tab to see the links to the Moodle sites to
which you already have access. Note that the majority of users with UofM
Guest IDs are not able to use myU portal at the moment.
2.
Via Moodle server: Go to http://moodle.umn.edu and login there with
either your Internet ID or Guest ID. Once logged in, you will be able to see
the links to your own sites and also will be able to browse and self-enroll in
other sites that are open for public access
3.
Via direct method: On your browser just go to the following site: https://moodle.umn.edu/course/view.php?id=11900
The
course open site is located at mnstats.morris.umn.edu//introstat/.
STATISTICAL COMPUTING:
The
link to the statistical packages that will be used in the course is located on
the course website. There are various alternative programs that you can choose.
We encourage you to use StatCrunch/WebStat. They are the same programs.
StatCrunch has enhanced version of WebStat and it is free. Passcode for the
StatCrunch is cougars. The information on how to use these programs will be
provided throughout the course.
COURSE ASSESSMENT:
As part of the Statistics
discipline's assessment plan, a pretest of important course concepts will be
given at the beginning of the term, and a post-test will be given at the end of
the course. These assessment exams are not used in determining your course
grade, but they are required to obtain a grade. No course work will be graded
until the pre-test is completed, and no course grade will be submitted to the
registrar until the post-test is completed. These tests are to be completed
electronically, and are available on the Moodle course page.
EXAMINATION
POLICY:
Three
midterm examinations and a final exam will be given. Time table and procedure
for the examinations is given below:
|
EXAMINATION 1 |
September 22-28 |
SCI. 3610 Outside Class |
8:00-9:05 am September 28, 11:55 pm |
|
EXAMINATION 2 |
October 22, (Friday) |
SCI. 3610 |
8:00-9:05 am |
|
EXAMINATION 3 |
November 22, (Monday) |
SCI. 3610 |
8:00-9:05 am |
|
FINAL |
December
15, (Tuesday) |
SCI.
3610 |
8:30-10:30
am |
EACH EXAMINATION
(INCLUDING THE FINAL) WILL BE CLOSED-BOOKS AND CLOSED-NOTES BUT YOU WILL BE
ALLOWED TO USE AN INFORMATION SHEET.
HOMEWORKS:
Nine
homeworks will be assigned. Homework
assignments will be given that correspond to each chapter in the text. Due
dates will be posted for each assignment on the Moodle course site. Several
problems will be given for each assignment, but only a few of them will be
assessed carefully with feedback provided. You will not be told in advance which
problems will be assessed. Late homework will be penalized 50% of the point
value. Students
need to download the assignment MS Word template from the course website, type
their answers and insert related graphs. All homework assignments are expected to be completed with a word processor
in electronic form. The assignments should be uploaded in Moodle course
website. Email submissions to the instructor will not be accepted.
|
INTRODUCTION TO THE PRACTICE OF STATISTICS Sixth Edition |
|
1. Looking at
Data: Distributions |
|
1.23,
1.24, 1.30, 1.117, 1.134, 1.140 |
|
2. Looking at
Data: Relationships |
|
2.9,
2.11, 2.41, 2.50, 2.66, 2.79, 2.95, 2.104, 2.131, 2.132 |
|
3. Producing Data |
|
3.4,
3.8, 3.24, 3.42, 3.54, 3.57, 3.60, 3.72, 3.116, 3.120, 3.128 |
|
4. Probability:
The Study of Randomness |
|
4.8,
4.24, 4.32, 4.33, 4.36, 4.56, 4.74, 4.89, 4.91, 4.101, 4.102, 4.116, 4.117,
4.128, 4.144 |
|
5. Sampling
Distributions |
|
5.12,
5.16, 5.28, 5.33, 5.36, 5.48, 5.66, 5.68 |
|
6. Introduction
to Inference |
|
6.26,
6.32, 6.52, 6.68, 6.69, 6.70, 6.78, 6.114 |
|
7. Inference for
Distributions |
|
7.24,
7.34, 7.41, 7.64, 7.80, 7.82 |
|
8. Inference for
Proportions |
|
8.16,
8.22, 8.24, 8.54, 8.64, 8.80 |
|
9. Analysis
of Two-Way Tables |
|
9.11,
9.20, 9.28, 9.35, Extra 9.34 |
|
10. Inference for
Regression |
|
10.33,
10.39, 10.53 |
|
11. Multiple
Regression |
|
TBA |
|
12. One-Way
Analysis of Variance |
|
12.29,
12.42, 12.45 |
|
13. Two-Way
Analysis of Variance |
|
TBA |
|
14. Nonparametric
Tests |
|
TBA |
MEDIA REPORT PROJECT: COMMUNITY-BASED RESEARCH
This
project will enhance your learning at the same time it will help to inform your
community. The detailed information on the project is located at the mnstats.morris.umn.edu/services/cst/statbook/.
COURSE
GRADE:
The
weights of homeworks midterm exams and final exam are given below.
|
HOMEWORKS: |
15% |
|
LEARNING
CHECKS: |
5% |
|
MIDTERM
EXAMS: |
50% |
|
FINAL
EXAM: |
30% |
|
GROUP
PROJECT: |
5%
(extra credit) |
|
A |
A- |
B+ |
B |
B- |
C+ |
C |
C- |
D+ |
D |
F |
|
90-100 |
88-89 |
86-87 |
80-85 |
78-79 |
76-77 |
70-75 |
68-69 |
66-67 |
60-65 |
0-59 |
S 68-100 N 0-67
COURSE PIN:
To view your progress in the course you need a
student PIN. To get your PIN please visit the course Moodle web-site, click on
the get
your pin button, and follow the instructions.
ORGANIZATION
OF IN-CLASS ACTIVITIES
The organization of the in-class activities are
summarized in the following flowchart. The main components of the organization
structure are:
(i)
Summaries and Outline: These two components, hopefully, will
provide a smooth transition between the topics and lectures. These will answer
three basic questions: Where have we been?, Where are we going?, and What have
we learned?
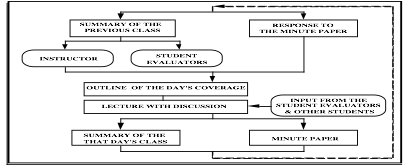
(ii) Student Evaluators: Class
participation and discussion are very important on the learning process.
Students are encouraged to ask questions in the class. Questions, comments
could help the instructor to set up his/her pace. The input from the students
should be constant. If you point out the weaknesses of the instructor, and the
problems with the course in general as soon as possible your learning process
will be enhanced. To formalize and promote active learning, each in-class
activity will be evaluated by the two students. These students will be
responsible to point out all the problems that might affect the learning of the
rest of the class. For example, the topics that are not clearly covered, pace
of the lecture, use of the blackboard, problems with taking notes, etc. Time
to time student evaluators will be asked to make a summary of the
previous class.
|
EVALUATOR |
DATE |
EVALUATOR |
DATE |
|
Abfalter,Chase
J |
8/25,27,30 |
Ranelli,Luciana
B |
10/4,6,8 |
|
Anderson,Collin
J |
9/1,3 |
Richards,Angela
Alice |
10/11,13,15 |
|
Buscher,Anastasia
F |
9/8,10 |
Schmeling,Cory
Michael |
10/20,22 |
|
Chen,Yitao |
9/13,15,17 |
Simon,Kenneth |
10/25,27,29 |
|
Dullinger,Kathryn
Amanda |
9/20,22,24 |
Spears,Brandon
L |
11/1,3,5 |
|
Faber,Alex |
9/27,29,
10/1 |
Stoll,Victoria
Lyn |
11/8,10,12 |
|
Fingalson,Travis |
10/4,6,8 |
Tang,Wenqing |
11/15,17,19 |
|
Halverson,Alicia
M |
10/11,13,15 |
Tangen,Oray
R |
11/22,23 |
|
Humphrey,Allie
Jean |
10/20,22 |
Thomas,Katelynn
Mae |
11/29, 12/1,3 |
|
Humphrey,Brita
J |
10/25,27,29 |
Workman,Samantha |
12/6,8,10 |
|
Johnson,Nicholas
A |
8/26,28,31 |
Young,Samuel
G |
11/1,3,5 |
|
Kamps,Heather
K |
9/1,3 |
Zabel,Jessica
Marie Fahrer |
11/8,10,12 |
|
Kernan,Danny
N |
8/25,27,30 |
Zdrazil,Matthew
D |
11/15,17,19 |
|
Li,Haimeng |
9/1,3 |
Zhang,Yiyue |
11/22,24 |
|
Li,Tianyue |
9/8,10 |
|
11/29,
12/1,3 |
|
Lindemann,Katherine |
9/13,15,17 |
|
12/6,8,10 |
|
Maudal,Sarah
Nicole |
8/25,27,30 |
|
10/4,6,8 |
|
McKye,Bridge |
9/1,3 |
|
10/11,13,15 |
|
McMullen,Wyatt
K |
9/8,10 |
|
10/20,22 |
|
Nelson,Jeremy
T |
9/13,15,17 |
|
10/25,27,29 |
|
Notch,Sean
Michael |
9/20,22,24 |
|
11/1,3,5 |
|
Novotny,Claren |
9/27,29, 10/1 |
|
11/8,10,12 |
|
Ortman,Elinor |
10/4,6,8 |
|
11/15,17,19 |
|
Prange,Brandon
J |
10/11,13,15 |
|
11/22,23 |
|
Qu,Minghui |
10/20,22 |
|
11/29,
12/1,3 |
DISABILITIES
AND MENTAL HEALTH
As a student you may experience a range of issues that can cause
barriers to learning, such as strained relationships, increased anxiety,
alcohol/drug problems, feeling down, difficulty concentrating and/or lack of
motivation. These mental health concerns or stressful events may lead to
diminished academic performance or reduce your ability to participate in daily
activities. University of Minnesota services are available to assist you
with addressing these and other concerns you may be experiencing. You can
learn more about the broad range of confidential mental health services
available on campus via http://www.mentalhealth.umn.edu/
.
![]()
0.
INTRODUCTION: DEFINITION AND USES OF STATISTICS
PART I
1. Looking at Data: Distributions
1.1
Displaying Distributions (excluding Time Plots)
1.2
Describing Distributions
1.3
The Normal Distributions (excluding Assessing Normality, Quantile and Normal
Plots)
2. Looking at Data: Relationships
2.1
Scatterplots
2.2
Correlation
2.3
Least-Squares Regression
2.4
Cautions about Regression and Correlation
2.5
The question of Causation
3. Producing Data
3.1
First Steps
3.2
Design of Experiments
3.3
Sampling Design
3.4
Toward Statistical Inference
PART II
4. Probability: The Study of
Randomness
4.1
Randomness
4.2 Probability Models
4.3
Random Variables
4.4
Mean and Variances of Random Variables
4.5
Probability Laws
5. Sampling Distributions
5.1
Counts and Proportions
5.2
Sample Means
PART III
6. Introduction to Inference
6.1
Estimating with Confidence
6.2
Tests of Significance
6.3
Use and Abuse of Tests (excluding Power and Inference as Decision)
7. Inference for Distributions
7.1
Inference for the Mean of a Population
7.2
Comparing Two Means
8. Inference for Count Data
8.1
Inference for a Single Proportion
8.2
Comparing Two Proportions
9. Inference for
Two-Way Tables
9.1 Data
Analysis for Two-Way (Relations in Categorical Data)
9.2 Inference for Two-Way Tables
9.3
Formulas and Models for Two-Way Tables
PART IV
10. Inference for Regression
9.1 Simple Linear Regression
11. Multiple Regression
12. One-Way Analysis of
Variance
13. Two-Way Analysis of
Variance
14. Nonparametric Tests
14.1 Wilcoxon Rank Sum Test
14.2
The Wilcoxon Signed Rank Test
14.3
The Kruskal-Wallace Test
PLEASE FEEL WELCOME TO SEE US OUTSIDE OF THE CLASS, ANY TIME, IF YOU HAVE QUESTIONS,
PROBLEMS, OR COMMENTS PERTAINING THE COURSE WORK.