FOR INSTRUCTORS USE
| 1. | a......./3 | b......./3 | c......./3 | d......./8 |
| e......./10 | f......./3 | ........../30 |
| 2. | a......../8 | b(i)......./4 | (ii)......./4 | (iii)......./4 | |
| ........../20 | |||||
| 3. | a......./7 | b......./7 | c......./6 | d......./5 | |
| ........../25 | |||||
| 4. | a......./6 | b......./7 | c......./7 | d......./5 | |
| ........../25 |
TOTAL ........../100
1. The accompanying data on milk volume (g/day) was taken
from the paper "Smoking During Pregnancy and Lactation and
Its Effects on Breast Milk Volume" (Amer. J. of Clinical
Nutrition, 1991, pp. 1011-1016):
| Smoking Mothers | |
| Nonsmoking mothers |
a. Describe the population(s) of interest to the researchers.
b. Identify the sample(s).
c. What is the variable of interest. Is this data qualitative or quantitative?
d. Construct a back-to-back stem-and-leaf display(s) of the data and interpret it.
e. Construct side-by-side boxplot for the data and interpret it.
f. Describe the inference that the researchers will make.
2.
a. A buyer of a lumber company must decide whether to buy a piece of land containing 5,000 trees. If 1,000 of the trees are at least 40 feet tall, the buyer will purchase the land; otherwise he won't. The owner of the land reports that the heights of the trees has a mean of 30 feet and a standard deviation of 3 feet. Based on this information, what is the buyer's decision? Please justify your answer.
b. The Hawaii Visitors' Bureau reports visitors coming to Hawaii from the U.S. mainland spend on the average of $102 per day (St. Petersburg Times, December 11, 1988). Assume the standard deviation is $27 and the distribution of expenditures is approximately bell-shaped.
(i) What percentage of the visitors will have an average daily expenditure of between $75 and $129 per day?
(ii) What percentage of the visitors will have an average daily expenditure of between $75 and $156 per day?
(iii) How much money a visitor should spend in order to
fall in the bottom 2.5% of all the visitors?
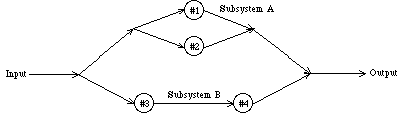
3. Consider the system of components connected as in the
accompanying picture. Components 1 and 2 in the Subsystem A are
connected in parallel, so that subsystem works iff either 1 or
2 works; since 3 and 4 in Subsystem B are connected in series,
that subsystem works iff both 3 and 4 work. The probability of
failure for components in subsystem A is .2, and the probability
of failure for components in subsystem B is .1. Assume components
operate independently of each other.

a. Find the probability that the system operates properly.
b. Find the probability that exactly one subsystem fails.
c. Find the probability that the system fails to operate properly.
d. Are the events "Subsystem A operates properly"
and "Subsystem B fails" mutually exclusive? Justify
your answer. (Yes or No will not receive any credit)
4. A certain company sends 70% of its overnight mail parcels via express mail service E. Of these parcels 2% arrive after the guaranteed delivery time. Suppose that remaining 30% of the overnight parcels are send via express mail service F. Of these parcels 10% arrive after the guaranteed delivery time.
a. Find the probability that a randomly selected parcel arrived late.
b. If a randomly selected parcel has arrived on time, what is the probability that it was sent via E.
c. Are the events "being on time" and "being send via F" independent? Justify your answer. (Yes or No will not receive any credit)
d. Suppose that the delivery of each parcels are independent.
Find the probability that at least two of the three parcels that
were send via F will arrive on time.