|
|
|
|
Random Walk:
Where is a drunk person going to end up?
Motivation: Scenario
Almost all of the issues that we are dealing in life can be modeled probabilistically so that we can easily understand the nature of the problems that we are facing better. In elementary probability models we assume that the possible outcomes for each experiment are the same and the outcome of one experiment does not influence the outcomes of the other experiments probabilistically. In some cases these assumptions are not valid. For example how much money you are going to have on your saving account next year depends on how much money you have on this account this year. Clearly next year's interest and unemployment rates will be affected by the this year's rates.
Big Question
Can we model a phenomenon where knowledge of the outcome of previous experiments influence our predictions for the outcomes of the next experiment?
Learning Objectives
To learn how to model chance processes for which the knowledge of previous outcomes influences prediction for future experiment. After completing this activity you should be able to construct a probability model for the cases where outcome in the future given the outcomes in the past and present depends only on the outcome that we observe in the present. You should also be able to see how different tools, such as tree diagrams, graphs, matrices, and tables, can be used to simplify the problem.
Background: Review, Definitions, Facts & Concepts
Markov chains that you are going to learn in this section is a type of a stochastic process which is a collection of random variables. One can represent a stochastic process as {X(t), t is in T} where for each t is in T, X(t) is a random variable. The index t is often interpreted as time and, as a result, we refer to X(t) as the state of the process at time t. T is called the index set of the process. When the index set is countable, the stochastic process is called a discrete-time process. If T is an interval of the real line, the stochastic process is said to be a continuous-time process. A discrete-time process is generally represented by Xn instead of X(t).
The state space of the stochastic process is the set of all possible values that the random variables X(t) can take which is represented by S. A realization of a stochastic process is called a sample path of the process.
Now, let us make sure that you understand these definitions. First an example.
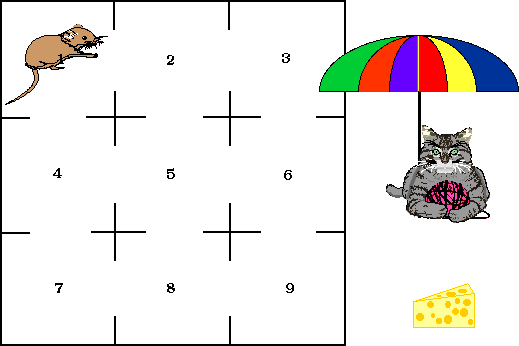
A Mouse in a Maze
A mouse starts from cell 1 in the maze shown below. A cat is hiding patiently in cell 7, and there is a piece of cheese in cell 9. In the absence of learning, when the mouse is in a given cell, it will choose the next cell to visit randomly from the adjoining cells. Assume that once the mouse finds the piece of cheese or the cat, it will understandably stay there forever.
|
|
|
|
Here is a sample path for this example:

|
Step (n) |
0 |
1 |
2 |
3 |
|
Xn |
1 |
2 |
3 |
2 |

|
Step (n) |
4 |
5 |
6 |
7 |
|
Xn |
5 |
4 |
5 |
8 |

|
Step (n) |
8 |
|
Xn |
7 |

What do you understand when one says
• X0=1
• X5=4
First of all, why is this a stochastic process?
The following matrix is called a one-step transition probability matrix.
What do you think that this matrix is representing?

The following matrix is called an incidence matrix.
What do you think that this matrix is representing?

The following graph is called a state diagram. What do you think that this graph is trying to tell us?
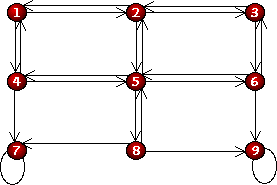
The following matrix is obtained by multiplying the matrix I by itself. If you do not understand how to multiply two matrices do not worry. Just tell us what you think that this matrix is representing.

The following matrix is obtained by multiplying the matrix I by itself three times. What do you think that this matrix representing?

The following matrix is obtained by multiplying the matrix I by itself four times. What do you think that this matrix representing?
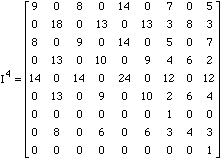
Suppose that the cat is on vacation and you are given the following incidence matrix.

Draw the maze (some of the doors between the cells are now closed)
Tell us where the cheese is.
Complete the following state diagram.
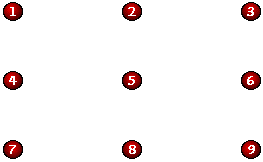
Do you think that drawing the above graph would help you to answer the last two questions?
Now, let us challenge ourselves. (I do not have slightest idea at this point whether this can be solved or not) This time it is the Cheese’s turn to take a vacation. You are given the following two-step incidence matrix.

Draw the maze.
Find where the cat is.
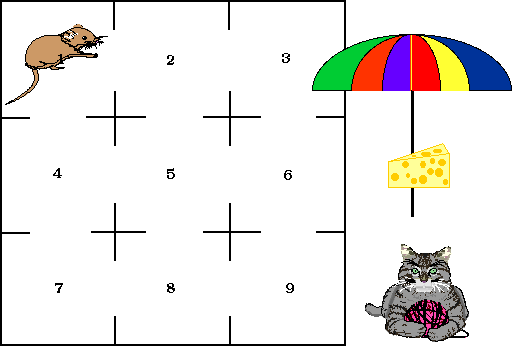
|
Learning Activity
Suppose that a person is walking along a four-block stretch of Park Avenue. The person starts at corner x and with probability 1/2, walks one block to the right and, with probability 1/2, walks one block to the left, when the person comes to the next corner she/he again randomly chooses her/his direction. The person continues until she/he reaches corner 4, which is a bar, or corner 0, which is a home. If the person reaches either home or the bar, she/he stays there. Here is a graphical representation of the problem.
|
|
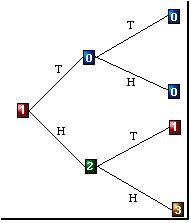
1. You will need a coin or other method of simulating an event with a probability 1/2. Pick a starting point 1, 2, or 3. Toss a coin. If the coin shows head move to the right, if it is tail move to the left. Continue tossing the coin until you reach to the bar or the home.
For example, if you get the following sequence and start at 1
H H T H T
Your position at each step will be
2 3 2 3 2.
Since you could not reach the bar of the home you should continue tossing the coin.
2.

a. Starting from 1, repeat the above experiment 10 times, fill out the following table, and record the number of times you ended up home and bar.
b. Starting from 2, repeat the above experiment 10 times, fill out the following table, and record the number of times you ended up home and bar.

c. Estimate you chance of reaching home starting from 1 by using the results of the experiments? What about your chance of reaching the bar?
Estimate you chance of reaching home starting from 2 by using the results of the experiments? What about your chance of reaching the bar?
Compare your results and justify why these estimates are different.
Connections
3. Tree Diagrams
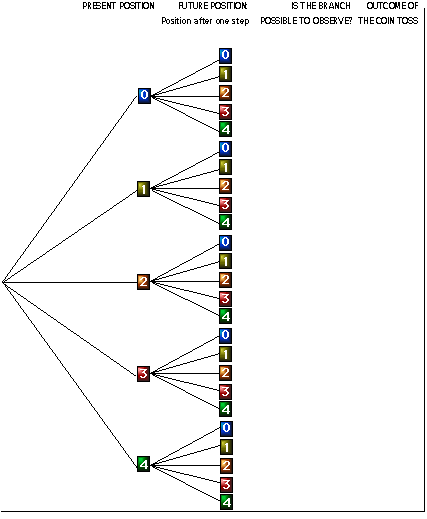
a. Consider the following tree which represents all possible outcomes of tossing a coin 4 times. Follow the individual branches and determine where the drunk person will be if she/he starts at 3.

b. Since, if the drunk person reaches either home or the bar, she/he stays there, eliminate the unnecessary branches of the tree diagram given above.
4. From Trees to Matrices
As you can see representing this problem in a compact form by using the trees is difficult. You have to be able to produce tree diagrams with infinite number of branches for each starting point. Now let us search for a better way of summarizing this problem.
a. Suppose that we saw this person at one of the blocks, the person had enough time to take only one step. Where this person will be when we come back? What are the factors that will affect your answer?
b.
c. Fill out the following table cross out the impossible steps, for the remaining ones put down the corresponding outcome of the coin toss experiment.
Replace corresponding outcomes of the experiment with the probability that matches. Now, we can represent the table of probabilities in a compact form as follows:

Interpret this matrix by referring to the table in c. This matrix is called one-step transition matrix. The states 0 and 4 are impossible to leave such states are called absorbing states. States which are not absorbing called transient.
Reaction and Reflection
5. Markov Property
Suppose that the drunk person was in block 1, then 2, then 1, then 2 and now the person is in block 3. You want to know where the person will be after the next step. Do you need to know that the person was in corners 1, 2, 1, 2, to determine where the person will be after visiting block 3?
6. What will Happen After Two or More Steps?
Suppose that the drunk person was in block 1, where this person could be after two steps? Construct a tree diagram to show possibilities. As an example we have given below a tree diagram when the drunk person was in block 1.
Fill out the following table cross out the impossible steps, for the remaining ones put down the corresponding outcome of the coin toss experiment. Note that this time we have to toss the coin two times.
Replace corresponding outcomes of the experiment with the probability that matches. Now, we can represent the table of probabilities in a compact form as follows:

Interpret this matrix which is called two-step transition matrix. Verify that

In fact if you want to know what will happen probabilistically after n steps, n-step transition matrix will be:
![]()
By using a calculator or MINITAB find the 4-step transition matrix and interpret.
MTB > read c1-c5
DATA> 1 0 0 0 0
DATA> 0.5 0 0.5 0 0
DATA> 0 0.5 0 0.5 0
DATA> 0 0 0.5 0 0.5
DATA> 0 0 0 0 1
DATA> end
5 ROWS READ
MTB > copy c1-c5 m1
MTB > print m1
MATRIX M1
1.0 0.0 0.0 0.0 0.0
0.5 0.0 0.5 0.0 0.0
0.0 0.5 0.0 0.5 0.0
0.0 0.0 0.5 0.0 0.5
0.0 0.0 0.0 0.0 1.0
MTB > multiply m1 m1 m2
MTB > print m2
MATRIX M2
1.00 0.00 0.00 0.00 0.00
0.50 0.25 0.00 0.25 0.00
0.25 0.00 0.50 0.00 0.25
0.00 0.25 0.00 0.25 0.50
0.00 0.00 0.00 0.00 1.00
MTB > multiply m1 m2 m3
MTB > print m3
MATRIX M3
1.000 0.000 0.000 0.000 0.000
0.625 0.000 0.250 0.000 0.125
0.250 0.250 0.000 0.250 0.250
0.125 0.000 0.250 0.000 0.625
0.000 0.000 0.000 0.000 1.000
MTB > multiply m1 m3 m4
MTB > print m4
MATRIX M4
1.000 0.000 0.000 0.000 0.000
0.625 0.125 0.000 0.125 0.125
0.375 0.000 0.250 0.000 0.375
0.125 0.125 0.000 0.125 0.625
0.000 0.000 0.000 0.000 1.000
Ongoing Assessment and Wrap-up
8. Give some examples where this process can be used in the real world.
Extensions
9. (Forecasting the weather) The chance of rain tomorrow depend on only today's whether. If it rains today, then it will rain tomorrow with probability 0.7 and if it does not rain today then it will rain tomorrow with probability 0.4. Form the one-step transition matrix.
Find the two-step transition probability matrix. What is the probability that it will rain two days from today given that it is remaining today?
Find the four-step transition probability matrix and interpret. Did you notice any interesting pattern in probabilities?
Answers:
![]()
![]()
![]()
10. (War of long distance companies) It has been observed that customers switch from one long distance company to another according to the following transition matrix.
![]()
Find the two-step transition matrix and interpret one and two-step transition matrices. Find the probability that a customer who uses MCI today will again be using MCI two months from today, assuming that she or he switches once a month.
![]()
![]()
Find the twelve step transition matrix. Interpret the matrix.
Answer:
![]()
11. (Gossip spreading) If a member of a
community is entrusted with some news, she/he will tell it to her/his
friends truly and without any changes with probability p. The probability
that she/he will twist it around and tell the opposite is really
negligible, say, ![]() . The
probability of such a misconduct and misbehavior is less than one in a
billion. Therefore, if a member of the community receives news, she/he
will tell it to another member truly and unchanged with probability
p, and she/he will twist it and tell its opposite with probability
. The
probability of such a misconduct and misbehavior is less than one in a
billion. Therefore, if a member of the community receives news, she/he
will tell it to another member truly and unchanged with probability
p, and she/he will twist it and tell its opposite with probability
![]() . Let
. Let
T= "the true statement about the young person's dog"
N= "the negation of the true statement about the person's dog".
Construct the one-step transition matrix. Interpret the matrix. Find ten, twenty, one hundred-step transition probability matrices. Do you see anything interesting? How are the probabilities changing? Can you say that in general in this community only half of the people is telling the truth?
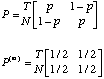
12. Visit the Mouse in a Maze example and place the cat so that the chance that the mouse will end up with cheese will be lower than the cat catching the mouse.