The important topics that you
should know for the exam.
6.3 Central Limit Theorem (CLT)
Sampling
distribution of 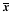
o The
standard deviation, standard error
- Approximate distribution of
the sample mean for large n (CLT)
Chp. 7 Estimation with Confidence Intervals
7.1 Large Sample Confidence intervals
for the m
7.2 Small Sample Confidence Intervals
for the m
7.3 Confidence Interval for a
Population Proportion, p.
7.4 Determination of Sample Size
For
the Population Mean
For
the Population Proportion
Chp. 8 Tests of Hypotheses
8.1 Elements of Tests of Hypothesis
8.2 Large Sample Test of Hypothesis
About m
8.3 Observed Significance Level:
P-Value
8.4 Small Sample Test of Hypothesis
About m
8.5 Test of Hypothesis About the
Population Proportion, p.
8.6 Calculating P(Type II Error) and
Power
8.7 Inference About a Population
Variance
STUDY
QUESTIONS FOR CHAPTERS 6, 7, and 8
1. In 1987, the average annual
rate of interest paid by savings and loan institutions in Pennsylvania was
7.26%. Assume a normal distribution and a standard deviation of 1.50% to answer
the following questions. What is the probability that a randomly selected 9
such institutions on the average paid between 7.00% and 8.00% interest on
deposits?
2. Unoccupied seats on flights cause airlines to lose revenue.
Suppose a large airline wants to estimate its average number of unoccupied
seats. To accomplish this, the records of 225 flights are randomly selected,
and sample mean is found to be 11.6 seats. Assume that the population standard
deviation is known to be 4.1 seats.
a. Estimate m= the
mean number of unoccupied seats per flight during the past year, using a 90%
confidence interval.
b. How large a sample needs to be
taken to estimate the mean number of unoccupied seats to within 0.35 seats with
90% confidence?
c. Test the hypothesis H0: m=13 seats
against the hypothesis Ha: m 13 at a=0.01
level.
d. Find the p-value of the test.
3. A method currently used by
doctors to screen women for possible breast cancer fails to detect cancer in
15% of the women who actually have the disease. A new method has been developed
that researchers hope will be able to detect cancer more accurately. A random
sample of 70 women known to have breast cancer were screened using the new
method. Of these, the new method failed to detect cancer in six.
a. State the null and
alternative hypotheses.
b. Define Type I and Type II
errors in the context of the problem.
c. Do the data provide
sufficient evidence to indicate that the new screening method is better than
the one currently in use? Use a=0.05.
d. Find the prob-value (p-value)
of the test
e. Using a 95% confidence
interval, estimate the proportion of the women with breast cancer that the new
method will fail to detect.
4. A
state game protector collects measurements on the weights of species of fish in
a lake. The standard deviation of the weights is known to be 2.13 pounds. A
total of 49 measurements are obtained and it is determined that sample mean is
7.34.
a. Give a 95% confidence interval
for the average weight of that species.
b. How many measurements must be
averaged to get a margin of error of 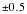 (with a bound of error of 0.5) (the mean to be within 0.5)
with 95% confidence?
(with a bound of error of 0.5) (the mean to be within 0.5)
with 95% confidence?
5. The manufacturer of a certain
foreign car sold in the United States claims that it will average 35 miles per
gallon of gasoline with the standard deviation of 9.3 miles. To test this
claim, a consumer's group randomly selects 40 of these cars and drives them
under normal driving conditions. These cars average 28 miles to the gallon.
Does this sample indicate that average mileage is more than 35?
a. State 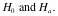
b. Carry out the test and give
the P-value. Report your conclusion.
c. Is the result significant at the
5% level (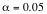 )?
)?
d. Find the probability of Type
II Error for mean 40.
e. Find the power of the test for
the mean 40.
6. A fast food restaurant is
considering a new product. It will be worthwhile to introduce this product if
the mean sales per store are more than $600 per week. In a marketing test the
product is sold at 26 stores. From the sample it is found that the mean
for weekly sales is $603.20 and
the standard deviation is $60.
a. State 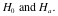
b. Carry out the test and give
the P-value. Report your conclusion.
c. Is the result significant at
the 5% level (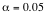 )?
)?
d. Give a 95% confidence interval
for the mean sales.
7. (Source: “Demons Begone”, Asheville Citizen-Times, April 5, 1991)
A poll of 1,226 adults revealed that 601 of them believe that the devil may
sometimes possess earthlings.
a. Construct a 90% confidence
interval for the true proportion of adults who believe that the devil may
sometimes possess earthlings.
b. Determine the sample size
required the estimate will be within 0.02 of the true proportion with 90%
confidence.
8. In May the fill weights of
"6-pound" boxes of laundry soap had a mean of 6.13 pounds with a
standard deviation of 0.095. The goal was to decrease the standard deviation.
The company decided to adjust the filling machines so that the standard
deviation will be reduced. In June a random sample of 20 boxes yielded mean of
6.10 and a standard deviation of 0.065.
a.
At a 0.05 significance level, was the company
successful?
b.
Set up a 99% confidence interval for s2.

![]()