Chp. 4 Discrete Random Variables
4.1 Types of random variables (Discrete and Continuous)
4.2 Probability distributions for discrete random variables
Construction of a
discrete probability distribution
Finding probabilities by
using a given probability distribution
4.3 Expected values of a discrete random variable
Finding mean, variance
and standard deviation
4.4 The binomial
random variable
Verifying
the characteristics of a binomial random variable
The
probability distribution of a binomial random variable
The
mean, variance and standard deviation of a binomial random variable
Finding
probabilities related with the binomial distribution
by using (i) Probability distribution p(x),
(ii) Binomial Tables
4.5 The Poisson
random variable
Verifying
the characteristics of a Poisson random variable
The
probability distribution of a Poisson random variable
The
mean, variance and standard deviation of a Poisson random variable
Finding
probabilities related with the Poisson distribution by using Poisson
probability distribution
Poisson
approximation to Binomial probabilities
Chp. 5 Continuous
Random Variables
5.1 Continuous
probability distribution
5.2 The uniform
distribution
The
probability distribution of a uniform random variable on the interval c to d
The
mean and standard deviation of a uniform random variable
Finding
probabilities for the uniform distribution by calculating the areas of the rectangles
5.3 The normal
distribution
Finding
probabilities for standard normal and general normal distribution
Given
probabilities, finding x, z, quartiles etc.
Use
of Normal Table
5.4 Normal
approximation to the binomial distribution
Steps
1-4 on pages 215
5.5 The exponential
distribution
The
probability distribution of an exponential random
variable
The
mean and standard deviation of an exponential random variable
Finding
the Area A to the right of a number a for an exponential distribution
SOLVING
PROBLEMS WHICH INVOLVES MORE THAN ONE PROBABILITY DISTRIBUTION
Chp. 6 Sampling Distributions
The
difference between parameter and statistics
6.1 Sampling
distribution
Finding
sampling distribution of a statistics
Finding
the mean and standard deviation of a sampling distribution
6.2 Properties of
sampling distribution
Point
estimator
Unbiased
estimate
Biased
estimate
Minimum
variance estimator
6.3 Central Limit
Theorem (CLT)
Sampling
distribution of 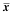
The
mean of 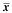
The
standard deviation of 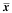 = standard error
= standard error
Approximate
distribution of the sample mean for large n (CLT)
EXAM II STUDY QUESTIONS
CHAPTER 4
1.
An employee of a firm has an option to invest $1,000 in the company’s bonds. At
the end of 1 year, the company will buy back the bonds at a price determined by
its profits for the year. From the past years, the company predicts it will buy
the bonds back at the following prices with the associated probabilities (x =
price paid for bonds):
|
x
|
$0
|
$500
|
$1,000
|
$1,500
|
$2,000
|
|
p(x)
|
.01
|
.22
|
.30
|
.22
|
.25
|
a.
What is the probability the employees will receive $1,000 or less for the
investment?
b.
What is the expected price paid for the bonds?
c. What
is the employee’s expected profit?
d.
Find the variance and standard deviation for this probability distribution.
2.
In a poll conducted by Parents magazine, 60% of parents said they wished they
had received more education (Parents, August 1988). A random sample of twenty
parents is selected.
a. What
is the probability distribution of x, the number of parents who hold this view
in this sample? Justify your answer.
b.
What is the expected number of parents who will hold this view in this sample?
What is the standard deviation of the random variable in part (a)?
c.
Find the probability that exactly 3 will
not hold this view in the sample.
d.
Use the normal approximation to find P(6<x<9).
3. A particular type of
birth-control pill is 90% effective. A random sample of 20 persons is selected.
a.
What is the probability distribution of x, the number of
unplanned births for this sample? Justify your answer?
b.
How many unplanned births would you expect in this sample?
What is the standard deviation of the random variable defined in part (a)?
c.
Find the probability that exactly 3 out of 20 will have unplanned births?
4. Consider
writing onto a computer disk and sending it through a certifier that counts the
number of missing pulses. Suppose this number X has a Poisson distribution with
mean 0.2. (Suggested in “Average Sample Number for Semi-Curtailed Sampling
Using Poisson Distribution,” J. Quality
Technology, 1993).
a. What
is the probability that a disk has exactly one missing pulse?
b. What is the
probability that a disk has at least two missing pulses?
5. For a recent period of
100 years, there were 93 major earthquakes ( at least 6.0 on the Richter scale)
in the world (based on data from the World
Almanac and Book of Facts). Assuming that the Poisson distribution is a
suitable model,
a.
Find the mean number of major earthquakes per year and the
standard deviation.
b.
Find the probability that the number of major earthquakes in
a randomly selected year is 5.
c. Find
the probability that the number of major earthquakes in a randomly selected
year is at least 2.
CHAPTER 5 & 6
6.
The speeds of all cars traveling on a stretch of Interstate Highway I-95 are
normally distributed with a mean of 68 miles per hour and a standard deviation
of 3 miles.
a. Find
the percentage of travelers who are violating the 65 miles speed limit.
b.
If a police officer decides to give a ticket to the fastest 10% of the drivers,
what should be the minimum speed he would use to write a speeding ticket?
c.
If a random sample of 36 cars traveling on this highway has been selected, what
is the probability that their average speed will exceed the 65 miles speed
limit?
7.
Based on the sample data collected in the Denver area, Nicholas Kiefer (1985)
found that in some cases the exponential distribution is an adequate
approximation for the distribution of the time (in weeks) an individual is unemployed. Use q
= 13 to answer the following questions.
a.
What is the mean time workers are unemployed according to the exponential
distribution?
b.
Find the probability that a worker
who just lost her job will be unemployed for at least two weeks.
c.
What is the probability that an unemployed worker will find a new job within 12
weeks?
d.
What is the probability that only two of the five unemployed workers will find
a new job within 12 weeks?
8.
In 1987, the average annual rate of interest paid by savings
and loan institutions in Pennsylvania was 7.26%. Assume a normal distribution
and a standard deviation of 1.50% to answer the following questions.
a.
What is the probability that a randomly selected Pennsylvania savings and loan
institution paid between 7.00% and 8.00% interest on deposits?
b.
What is the probability that a randomly
selected 9 such institutions on the average paid between 7.00% and 8.00%
interest on deposits?
c.
What is the probability that only 5 of the 9 such institutions paid between
7.00% and 8.00% interest on deposits?
9.
In deciding how many customer service representatives to
hire an in planning their schedules, it is important for a firm marketing
electronic typewriters to study the repair times for the machines. Such a study
revealed that repair times have an exponential distribution with q=22
minutes
a.
What is the expected repair time for
an electronic typewriter?
b. Find the probability that a repair time
will last less than 10 minutes.
c.
The charge for typewrite repair is $50 for each half hour, or part thereof, for
labor. What is the probability that a repair job will result in a charge for
labor of $100?
10.
The board of examiners that administered the real estate
brokers' examination in a certain state found that the mean score on the test
was 435 and the standard deviation was 72. If the board wants to set the
passing score so that only the best 30% of all applicants pass, what is the
passing score? Assume that the scores are normally distributed.
11.
A taxi service based at an airport can be characterized as a
transportation system with one source terminal and a fleet of vehicles that
take passengers from the terminal to different designations. Each vehicle
returns to the terminal after some random trip time and makes another trip. To
improve the vehicle-dispatching decisions involved in such system, Sims and
Templeton (1985) assumed travel times of successive trips are independent
exponential random variables to model the system. Assume q
= 20 minutes.
a.
What is the mean trip time for the taxi service?
b.
What is the probability that a particular trip will take less than 30 minutes.
c.
What is the probability that a particular trip will take
between 10 to 15 minutes.
d.
Two taxis have just been dispatched. What is the probability
that both will be gone for more than 30 minutes? That at least one of the taxis
will return within 30 minutes?
CHAPTER
6
12. A state game protector
collects measurements on the weights of species of fish in a lake. Suppose that
the weight has a normal distribution with mean 7.34 and a standard deviation of
2.13 pounds. A total of 49 measurements are obtained.
a.
What is the sampling distribution of the average weight of
49 fish?
b.
What is the probability that a randomly selected fish will
weigh more that 7.5 pounds?
c.
What is the probability that the average weight of 49 fishes will exceed 7.5 pounds?
d.
Suppose that the weight of fish has a mean 7.34 and standard
deviation 2.13. But the distribution of the weight is unknown. What are your
answers to a, b, and c.
