STATISTICAL METHODS

INFORMATION ON THE FIRST MIDTERM EXAMINATION

Date: September 21, 2011 (Wednesday)

Time: 9:15-10:20

Place: SCI. 3550

Examination Type: Closed notes and books. But you will be allowed to use one sheet of paper (information sheet) with the formulas and facts that you need (This sheet should not have solutions of problems or examples)

Coverage: Chapter 1-3

The important topics that you should know for the exam.

Chp. 1 Statistics

1.1 & 1.2. Definition of statistics & Types of Statistical Applications

descriptive and inferential statistics

1.3. Elements of Statistics

population

variable

sample

statistical inference

reliability of the inference

1.4. Types of Data

Qualitative, Quantitative; nominal, ordinal, interval, ratio data

1.5. Collecting Data

Chp. 2 Descriptive Statistics

2.1. Describing Qualitative Data

2.2. Graphical methods for quantitative data

Stem-and-leaf displays and its interpretation

Histograms and its interpretation

2.3 & 2.4 Measures of Central Tendency

sample mean and population mean (μ)

How to find mean

How to find median (position and depth of the median)

How to find mode (unimodal, bimodal, multimodal).

2.5. Measures of variability

Why do we need a measure of dispersion?

sample range

sample mean absolute deviation

sample variance

sample standard deviation( why do we need sample standard deviation?)

2.6. Interpreting and Understanding standard deviation

Chebyshev's Theorem (for all distributions)

Emprical Rule (for normally distributed data)

(Given mean and standard deviation find the proportion of observations between two values, find

the limits given the percentages)

2.7. Measures of relative standing (position)

Percentiles & Quartiles

z-scores (how to find z-scores, use of z-scores, interpretation of z-scores)

2.8. Methods of Detecting Outliers, Boxplots

IQR= Q_U-Q_L

Construction of the boxplots by using lowest value, lower quartile, median, upper quartile,

highest value

Interpretation of single and side-by-side boxplots

Chp. 3 Probability

3.1. Elements of Probability

experiment, simple event, sample space, event

steps for calculating event probabilities

3.2 & 3.4. Compound events

unions and intersections

3.3. Complementary events (How to find the probability of a complement of an event)

3.5. Conditional probability & the Bayes rule

3.6. Probabilities of Unions and intersections

additive rule

multiplicative rule

mutually exclusive events & independent events (showing whether two events are mutually

exclusive or independent and given mutually exclusiveness and independents finding compound

event probabilities

3.7. Random Sampling

3.8. Some Counting Rules

STUDY QUESTIONS

1. Here is the number of home runs that Babe Ruth and Roger Maris hit during the years that they were with the New York Yankees.

BABE RUTH

ROGER MARIS

Note that Ruth's record of 60 home runs in one season was broken by another Yankee, Roger Maris, who hit 61 home runs in 1961.

a. What is the variable of interest? Is this data qualitative or quantitative?

b. Produce a back-to back stem-and-leaf display for the home runs of Babe Ruth and Roger Maris and interpret. Who was superior as a home run hitter?

c. Construct boxplot for the home runs of Babe Ruth and interpret it.

2. a. A survey of local companies found that the mean amount of travel allowance for executives was $0.25 per mile. The standard deviation was $0.02. Using the Chepyshev's theorem, find the minimum percentage of the data values that will fall between $0.20 and $0.30.

b. The distribution of amounts spent per month for rent by students attending Computer University is mound-shaped. The mean monthly rental is $450, and the standard deviation is $125. approximately, what percentage of rentals is between $75 and $825?

3. The security manager of a large building reports that the probability is 0.05 that a fire alarm will not operate when needed. Suppose that there are 3 alarms in the building, and whether one operates or not does not affect the operation of others.

a. What is the probability that all of them will operate during a particular fire?

b. What is the probability that at least 1 will operate during a particular fire?

4. At a large factory 89 employees were surveyed and classified according to their level of education and whether or not they smoked. The data are shown in the table.

	Educational level
Smoking Habits	Not high school graduate	High school graduate	College graduate
Smoke	6	14	19
Do not smoke	18	7	25

A. If an employee is selected at random, find these probabilities

a. the employee is a high school graduate and smokes

b. the employee smokes, given that s/he graduated from college

c. given that the employee smokes, s/he is a college graduate

d. Are the events "smoke" and "not high school graduate" independent? Please justify your answer.

5. A pregnancy test is 98% accurate in detecting pregnancy. That is, if a woman is pregnant, it will show positive 98% of the time and show negative 2% of the time. Furthermore, if a woman is not pregnant, it will show negative 98% of the time and positive 2% of the time. Assume that there is a 50% probability that a woman who uses the test is pregnant.

a. Find the probability that the test will be negative.

b. Find the probability that if the test shows positive, the woman is nor pregnant.

6. Consider the following system of components connected as in the accompanying pictures. The probability of failure for components in the system is 0.1. Assume components operate independently of each other.

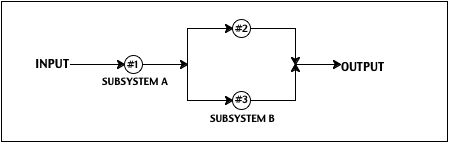
a. Find the probability that the system will fail to operate properly.

b. Find the probability that at lease one of the subsystems will fail.