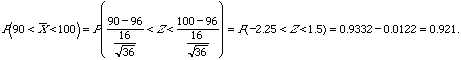1. Three different road-repair compounds were tested at four different locations. At each location, three sections of the road were repaired, with each section using one of the three compounds. Data were collected on the number of days of traffic usage before additional repair was required.

Define the experimental units, factor(s), levels of the factors, treatments, and the response variable.

Discuss whether or not the three principals of design of experiments are satisfied.

2. A major metropolitan police force in the Eastern United States studied the relationship between gender and getting a promotion. The following table provides the associated probabilities:

a. What is the probability that a randomly selected officer is promoted? P(A)=0.25+0.03=0.27

b. What is the probability that a randomly selected officer is promoted or female? P(A or B)=0.27+0.20-0.03=0.44

c. What is the probability that a randomly selected officer is female and is not promoted? P(B and A^C)=0.17

d. What is the probability that a randomly selected officer is promoted given a female officer? P(A|B)=0.03/0.20=0.15

e. What is the probability that a randomly selected officer is promoted given a male officer? P(A| B^C)=0.24/0.80=0.30

f. Are the events "being promoted" and "being female" disjoint? Are they independent? Please justify your answer to receive a credit. Not disjoint, because P(A and B)=0.03 not 0. P(A and B)=0.03, P(A)P(B)=0.27x0.20=0.054. Since P(A and B) is not equal to P(A)P(B), the events are not independent.

3. A somewhat absent-minded hiker forgets to bring her insect repellent (A) on 30% of his hikes. The probability of being bitten (B) is 90% if she forgets the repellent, and 20% if she uses the repellent.

a. What is the probability that she will be bitten? P(B)=(0.30)(0.90)+(0.70)(0.20)=0.27+0.14=0.41

b. What is the probability that she forgot her repellent given that she was bitten? P(A|B)=P(A and B)/P(B)=0.27/0.41=0.6585

4. The probability distribution for the number of toppings, in addition to cheese, ordered on a pizza is

a. Determine the mean. m=0(0.3)+1(0.4)+2(0.2)+3(0.06)+4(0.04)=0.4+0.4+0.18+0.16=1.14

b. What is the probability that a customer will not order any topping? 0.30

c. Find P(1<x_3). P(1<x_3)=P(x=2)+p(x=3)=0.2+0.06=0.26

5. Public Opinion reported that 5% of Americans are afraid of being alone in a house at night. Suppose that a random sample of 20 Americans is selected.

a. Find the mean and standard deviation of the number of Americans who are afraid of being alone in a house at nigh out of 20 Americans.

b. What is the probability that exactly five people in the sample of 20 are afraid of being alone at night? P(X=5)=0.0022

c. What is the probability that at most three people in the sample of 20 are afraid of being alone at night? P(X_3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)=0.3585+0.3774+0.1887+0.0596=0.9842

d. Used the Normal approximation to find the probability that the proportion of the people who are afraid of being alone at night in a random sample of 64 patients will be at least 6%. n=64, p=0.05

6. The average age of a vehicle registered in the United States is 96 months. Assume the standard deviation is 16 months. Assume the average of a vehicle has a normal distribution.

a. Find the probability that a randomly selected vehicle will have an age greater than 100 months.

b. If a random sample of 36 cars selected, Find the probability that the average age is between 90 and 100 months.