UNIVERSITY OF MINNESOTA, MORRIS

INTRODUCTION TO MATHEMATICAL STATISTICS

MATH. 3611

SPRING, 1997

1. Let and be idependent samples from a normal distribution with and

a) What is the distribution of

b) What is the distribution of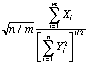

c) What is the distribution of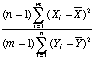

d) Suppose that m=9 and n=4. Determine c such that

2. In a survey to determine the total value of the homes in a particular community a simple random sample of n=20 homes is selected from the 1000 homes in the community. From the tax records the investigator obtains the assessed value for this year (x) for each of the 20 homes included in the sample. The following data is obtained from the survey (figures in $10,000): The total value of 20 homes in the sample is 164.7 with a sample standard deviation 0.957.

a) Give an unbiased estimates of the avearage value of the homes, and the total value of the homes in the community.

b) Construct an approximate 99% confidence interval for the population total.

c) How large the sample be in order that the 95% confidence interval for the total value of the homes in the community will have a width of 300 (ignore the finite population correction factor in answering this question).

3. In a university with total 2000 freshmen and 1500 seniors a survey was conducted to assess the overall educational perspective of the students. Of a sample of 200 freshmen, 90 reported that they had no writing experience in any of their classes during the last year. Of 185 seniors, 65 reported that they had no writing experience in any of their classes.

a. Estimate the proportion of freshmen in this university who did not have a writing experience and construct a 95% confidence interval for this proportion.

b. Let pbe the population proportion of the freshmen who did not have writing experience, and pbe the population proportion of the seniors who did not have writing experience. Estimate p-pand construct a 90% confidence interval for this difference.

c. What should be the sample size for seniors so that the standard error of pwill be less than 0.021. (Ignore the finite population correction factor)

d. Estimate the total number of seniors in the population who did not have a writing experience and construct a 95% confidence interval for this total.

4. It is desired to test whether the number of gamma rays emitted per second by a certain radioactive substance is a random variable having Poisson distribution. Use the following data obtained for 300 one-second intervals to fit a Poisson distribution and test goodness of fit using Pearson's chi-square statistics.

5. Let be i.i.d. random variables from a distribution with the following probability density function

b) Is the method of moments estimator unbiased? Please justify your answer. (Only yes/no answer will not receive any credit)

6. Let be i.i.d. random variables from a distribution with the following probability density function

a) Find a sufficient statistic for .

b) Find the maximum likelihood estimator of .

c) Find the asymptotic variance of the maximum likelihood estimator.

7. Let X have one of the following distributions:

a) What is the likelihood ratio test of versus at level ?

b) Suppose that a test rejects if X=4, 5, or 6. What is the significance level (probability of type I error) of the test?

c) Find the power of the test given in (b).

8. Suppose that has the following probability density function

a) Consider the test that rejects in favor of for What is the significance level of the test?

b) Consider the test that rejects in favor of for What is the power of the test?

c) Let be a sample from this distribution. Find the likelihood ratio for testing versus , where