|
|
UNIVERSITY OF MINNESOTA, MORRIS
INTRODUCTION TO MATHEMATICAL STATISTICS
MATH. 3611
SECOND MIDTERM EXAMINATION
SPRING, 1997
|
|
NAME:........................................................................
ID #:............................................................................
THE EXAM WAS ...........EASY ..........FAIR ..........DIFFICULT
FOR INSTRUCTORS USE
|
1 |
a....../8 |
b....../9 |
c......./8 |
|
........./25 |
|
|
2 |
........./20 |
|||||
|
3 |
........./20 |
|||||
|
4 |
a....../9 |
b....../9 |
c......./8 |
d....../9 |
........./35 |
|
|
TOTAL |
......./100 |
1.
A seafood wholesaler selected random samples of n=n=n=400 households from each of the three markets (strata) and obtained from each household an estimate of the dollar amount spent per month on seafood. The number of households in each market along with the sample means and population variances are shown in the table.|
NEIGHBORHOOD |
N |
SAMPLE MEAN |
POPULATION VARIANCE |
|
1 |
20,800 |
$5.31 |
16 |
|
2 |
6,400 |
$9.49 |
9 |
|
3 |
12,600 |
$6.75 |
25 |
a.
Estimate the total amount spend per month on seafood in the city.b. For a sample of 1200, determine the sample sizes for the proportional allocation.
c. For a sample of 1200, determine the sample sizes for the optimal allocation.
2. A study of sterility in the fruit fly ("Hybrid Dysgenesis in Drosophila Melanogaster: The Biology of Female and Male Sterility", Genetics, 1979) reports the following data on the number of ovaries developed for each female fly in a sample of size 1388.
|
n |
frequency |
|
0 |
1212 |
|
1 |
118 |
|
2 |
58 |
|
3+ |
0 |
Fit a Poisson distribution and test goodness of fit using Pearson's chi-square statistics.
(HINT: Note that if X is the number of component failures,
)
3.
Let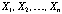 
be i.i.d. random
variables from a uniform dstribution on [q-2,q+2], that is
Find the method of moments estimate of
q.
4. Let X1, X2, ..., Xn be i.i.d. random variables with the density function
a)
Find the maximum likelihood estimator of
.
b) Find the asymptotic variance of the maximum likelihood estimator.
c) Form an asymptotic (1-a)100% confidence interval for the maximum likelihood estimator.
d) Does this distribution belong to the exponential family? Please justify your answer.
Find a sufficient statistics for .
