|
|
UNIVERSITY OF MINNESOTA, MORRIS
INTRODUCTION TO MATHEMATICAL STATISTICS
Math. 3611
|
|
FIRST MIDTERM EXAMINATION
SPRING, 1997
NAME:........................................................................
ID #:............................................................................
THE EXAM WAS ...........EASY ..........FAIR ..........DIFFICULT
FOR INSTRUCTORS USE
|
1 |
a....../7 |
b....../8 |
c...../10 |
........./25 |
||
|
2 |
a....../10 |
b....../10 |
c...../10 |
........./30 |
||
|
3 |
........./15 |
|||||
|
4 |
a....../7 |
b....../7 |
c...../8 |
d...../8 |
......../30 |
|
|
TOTAL |
......../100 |
1. Let 
be a
sample from an 
, 
be an independent sample from an
distribution, and Z has
a standard normal distribution and independent of 
a. What is the distribution of 
? Justify your answer.
b. What is the distribution of 
? Justify your answer.
c. What is the distribution of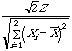 
? Justify your answer.
d. Find 
.
2.
A survey is carried out in a city of 10,000 population. It is found that 69 of a random sample of 100 individuals favored a law requiring a teenager to have her parents' consent before having an abortion.a. Define the parameter of interest for this survey and give an unbiased estimate of this parameter.
b. Find a 90% confidence interval for the parameter that you have defined in (a).
c. How large should the sample be in order for the standard error of the estimate of the population proportion to be less than 0.015? (Ignore the finite population correction in answering this question).
3. Three independent surveys independently conducted to estimate
the population proportions 
,
respectively. It is known that 
. Denote the corresponding sample proportions by 
. For some 
, the three estmates are combined to give a better
estimator of 
;
.
Find the condition on 
that
make 
an unbiased estimator of
.
4. Resources managers of forest game lands want to estimate the size of the deer population in a particular forest. From an aerial photograph the forest was divided into 10,000 30-foot-square grids. In 1991 a simple random sample of 500 plots was taken and the number of pellet groups was observed for deer . The experiment was repeated in 1992 by taking a simple random sample of 400 plots. The results
The results are given in the following table.
|
YEAR 1991 |
YEAR 1992 |
|
Sample mean=2.30 |
Sample mean=2.20 |
|
Sample variance=0.65 |
Sample variance=0.97 |
a.
Give unbiased estimates of the population means (m, and m) and population totals (t, and t) for 1991 and 1992, respectively.b. Construct a 99% confidence interval for
m.c. Construct a 95% confidence interval for
m- m.d. How large the sample be in order that the 95% confidence interval for the total number of deer in 1992 will have a width of 500 (ignore the finite population correction factor in answering this question).
