II. Suppose that P(E)=0.7, P(F)=0.5, and
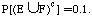 Find the following:
Find the following:
a. P(E»F)
b. P(E«F)
c. P(E|F)
d. P(F|E)
|
|
FOR INSTRUCTORS USE
1. I........./5
II.a......../4 b......./4 c......./4 d......./4
III........./4 ........../25
2 a......./10 b......../10 ........../20
3. a....../10 b......../5 c....../5 d........./5 ........../25
4. a....../8 b....../7 ........../15
5. a....../5 b......../5 c....../5 ........../15
TOTAL ........../100
1. I. Suppose that we roll two dice. What is the probability that the sum is 7 given that neither die showed a 6? |
HINT: The sample space for the experiment is
II. Suppose that P(E)=0.7, P(F)=0.5, and 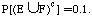 Find the following: Find the following:
a. P(E»F) b. P(E«F) c. P(E|F)
d. P(F|E) |
III. Suppose that the probability of living to be older than 70 is
0.6 and the probability of living to be older than 80 is 0.2. If a person
reaches her 70th birthday, what is the probability that she will
celebrate her 80th? |
2. An urn contains three red and two white balls. A ball is drawn, and then it and another ball of the same color are placed back in the urn. Finally, a second ball is drawn. a. What is the probability that the second ball drawn is white?
b. If the second ball drawn is white, what is the probability that
the first ball drawn was red? 2. Of the travelers arriving at a small airport, 60% fly on major airlines, 30% fly on privately owned planes, and the remainder fly on commercially owned planes not belonging to a major airline. Of those traveling on major airlines, 50% are traveling for business reasons, whereas 60% of those arriving on private planes and 90% of those arriving on other commercially owned planes are traveling for business reasons. Suppose that we randomly select one person arriving at this airport, what is the probability that the person a. is traveling on business?
b. arrived on a privately owned plane given that the person is
traveling for business reasons? |
3. Suppose that a balanced coin is independently tossed two times. Define the following events: E= head appears on the first toss F= head appears on the second toss G= both tosses yield the same outcome a. Are E, F, and G independent? Please show your work and justify your answer. b. Are the events E and G mutually exclusive? Please show your work and justify your answer. c. What is the probability that at most one of the three events occurs? d. What is the probability that all three events occur? |
4. If the cumulative distribution function (cdf) of a random variable X, F, is given by
a. Compute P(X<3), P(X£3.2), P(X"1.2), and P(-2<X"3.2).
b. Calculate the probability mass function of X. |
5. Suppose we draw 3 balls out of an urn with 5 red and 4 black balls. Let X be the number of red balls drawn. a. What are the possible values of X? b. Determine the probability mass function of X. c. Determine the cumulative distribution function of X. |