1.
a. Let P(A|B)=0.3 and P(B|A)=0.6, and P(A«B)=0.3. Find
P(A) and P(B).
b. Let P(A|B)=0.7, P(A«B)=0.2, and
P(Ac)=0.3. Find 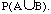
|
|
PROBABILITY THEORY |
1.
a. Let P(A|B)=0.3 and P(B|A)=0.6, and P(A«B)=0.3. Find
P(A) and P(B).
b. Let P(A|B)=0.7, P(A«B)=0.2, and
P(Ac)=0.3. Find |
2. Binary digits 0 and 1 are transmitted over a communications channel. If a 1 is sent, it will be received as a 1 with probability 0.95 and as a 0 with probability 0.05; if a 0 is sent, it will be received as a 0 with probability 0.99 and as a 1 with probability 0.01. If the probabilities that a 0 or a 1 is sent are equal, what is a. the probability that a1 will be received.
b. the probability that a 1 was sent given that a 1 was
received?
|
|
RANDOM VARIABLES |
PLEASE ANSWER EITHER ONE OF THE FOLLOWING TWO QUESTIONS 3. Suppose that the random variable X has the following probability density function
 a. Find E[X]. b. Find Var[X]. c. Find P(X>1.5).
(Extra Point Question) d. Find 3. Suppose that the random variable X has the following probability density function
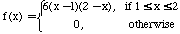 a. Find E[X]. b. Find Var[X]. c. Find P(X>1.5).
(Extra Point Question) d. Find |
4. (Use the moment generating function to answer the following questions) a. Suppose that X has a Binomial distribution with n=1 and p=0.5. What is the moment generating function of Y=1-2X?
b. Suppose that X, Y and Z are independent
Binomial random variables with parameters
(nX=5,p X=0.9), (n Y=10, p
Y=0.9) and (nZ=25, p Z=0.9) respectively.
What is the distribution of X+Y+Z?
|
5. Let X and Y be continuous random variables with joint probability density function given by
 a. Find the marginal probability density function of X and the marginal density function of Y.
b. Determine if X and Y are independent.
|
|
CONDITIONAL PROBABILITY & CONDITIONAL EXPECTATION |
6. (Please note that the joint probability density function given in this problem is same as Question 5) Let X and Y be continuous random variables with joint probability density function given by
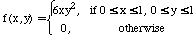
a. Find the conditional probability density function of X
given Y=y (that is b. Find E[X | Y= ]. |
PLEASE ANSWER EITHER ONE OF THE
FOLLOWING TWO QUESTIONS 7. (The Thief of Baghdad Problem)
The Thief of Baghdad has been placed in a
dungeon with three doors. One of the doors leads into a tunnel which
returns him to the dungeon after one day's travel through the tunnel.
Another door leads to a similar tunnel whose traversal requires three
days rather than one day. The third door leads to freedom. Assume that
the thief is equally likely to choose each door each time he makes a
choice. Find the expected number of days the thief will be imprisoned.
7. A taxi repeatedly circles past a certain point, using
one of the two routes. Route 1 requires 4 minutes to complete and is used
with probability 0.6, while Route 2 takes 7 minutes and is used with
probability 0.4. Assume that the taxi has probability 0.1 of getting a
fare at the point each time it passes and that this is the only source of
fares for the taxi. Given that the empty taxi has just passes the point,
what is the expected length of time required before the taxi gets a fare?
|
|
MARKOV CHAINS |
8. A fugitive moves about two cities Galveston and Sugarland to escape a bounty hunter. The fugitive makes the move at the end of each day. If the fugitive is in Galveston, then she/he moves to Sugarland with probability 0.8; if she/he is in Sugarland, then she/he moves to Galveston with probability 0.3. a. Determine the probability transition matrix. b. Suppose that the fugitive is in Sugarland find the probability that find the probability that she/he will be in Sugarland two days after. c. After sufficiently long time, what is the probability that the fugitive will be in Galveston? Sugarland? |