1.
a. If a student selects answers randomly and independently on a
true-false examination, determine the probability that the first correct
answer is that of question 3.
b. A pediatrician wishes to recruit 5 couples, each of whom is
expecting their first child, to participate in a new natural childbirth
regimen. Suppose that the probability of selecting a couple who agrees to
participate is 0.2. What is the probability that 8 couples must be asked
before 5 are found who agree to participate?
c. A doctor has five patients with migraine headaches. She
prescribes for all five a drug that relieves the headaches of 82% of such
patients. What is the probability that the medicine will
not relieve the headaches of two of these patients?
| 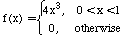
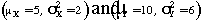 , respectively. What is the
distribution of X+Y?
, respectively. What is the
distribution of X+Y?