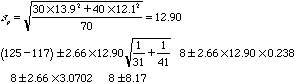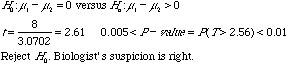SOLUTIONS TO THE THIRD EXAM
FALL, 1999

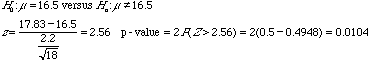 . Reject the null hypothesis at 0.05 level.
. Reject the null hypothesis at 0.05 level.
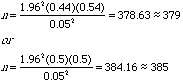
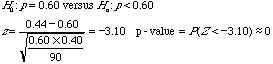
3. Suppose you want to test ![]() using
using
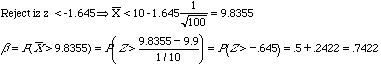
Power is 1-0.7422=0.2578.
PLEASE ANSWER EITHER ONE OF THE FOLLOWING TWO QUESTIONS
4. A new kind of typhoid shot is being developed by a medical research team. The old typhoid shot was know to protect the population for a mean of 36 months with a standard deviation of 3 months. To test the variability of the new shot, a r andom sample of 24 people was given the new shot. The regular blood tests showed that the sample standard deviation of protection time was 1.9 months.
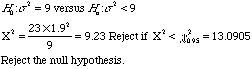
The shot has a smaller variance of protection times.
![]()
4. A group of environmentalists claims that the warm water from Virginia Power plant at Lake Anna is limiting the growth of striped bass at the lake. In a similar southeastern reservoir the average weight of striped bass is 25 pounds with a sta ndard deviation of 8 pounds. A study of 30 striped bass at the Lake Anna revealed a mean weight of 20 pounds.
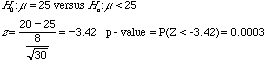
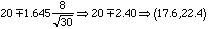
5. A biologist suspected that males age 20-24 have a higher mean systolic blood pressure than females in the same age group. Independent random samples of males and females were selected from the Framingham Heart Study. The data are as follows:
|
n |
|
s |
|
|
Males |
31 |
125 |
13.9 |
|
Females |
41 |
117 |
12.1 |