MATHEMATICS DISCIPLINE
UNIVERSITY OF MINNESOTA, MORRIS
MORRIS, MN 56267
![]()
FIRST MIDTERM EXAMINATION
FALL, 1999
1. The Age Discrimination in Employment Act mandates that workers 40 years of age or older be treated without regard to age in all phases of employment (hiring, promotions, firing, etc.) During the recession of the early 1990s, a small computer manufacturer laid of 10 of its 20 software engineers. The ages of all the engineers at the time of layoff are shown in the table.
|
Not laid off |
Laid off |
|
34 |
52 |
|
55 |
35 |
|
42 |
40 |
|
38 |
41 |
|
42 |
40 |
|
32 |
39 |
|
40 |
40 |
|
40 |
64 |
|
46 |
47 |
|
29 |
44 |
a. What is the variable of interest. Is this data qualitative or quantitative?
b. Produce a back-to back stem-and-leaf display for the ages of Not laid of and Laid off employees and interpret.
c. Construct boxplot for the ages of Laid off employees and interpret it.
2.
a. Dr. Thomas Stanley of Georgia State University has collected information on millionaires, including their ages, since 1973. A sample of 36 millionaires has a mean age of 58.5 and a standard deviation of 13 years. Using the Chepyshev's theorem, f ind the minimum percentage of millionaires with an age between 39 and 78 years.
b. The number of vehicles passing through a certain intersection has a mound-shaped distribution with a mean of 375 vehicles per day and a standard deviation of 25 vehicles. What can you say about the percentage of the days that more than 425 ve hicles used the intersection?
c. The hourly wages of 2 people working in the trades are to be compared. Neil Holzmann, a carpenter, earns $12.00 per hour. Joe Bevilacqua, a plumber, earns $16.00 per hour. A survey of both trades in the same city reveals the following informa tion:
|
|
Plumber |
Carpenter |
|
Mean |
$15.00 |
$10.00 |
|
Standard Deviation |
$1.75 |
$1.25 |
Compare the relative positions of the two tradesmen within their respective trades. (That is, decide which one of these tradesmen is earning more money relative to their respective trades).
3. In a letter to the editor that appeared in the February 23, 1987, issue of U.S. News and World Report, a reader discussed the issue of space shuttle safety. Each "criticality 1" item must have 99.99% reliability, according to NASA standar ds. This means that the probability of failure for a "criticality 1" item is only 0.0001. Mission 25, the mission in which the Challenger exploded, had 748 "criticality 1" items. Suppose that whether one item fails or not does not affect the operation of other items.
a. Determine the probability that none of the "criticality 1" items would fail.
b. Determine the probability that at least one of the "criticality 1" items would fail.
4. A major metropolitan police force in the Eastern United States studied the relationship between gender and getting a promotion. The following table provides the associated probabilities:
|
|
GENDER |
|
|
Female |
Male |
|
|
Promoted |
0.03 |
0.24 |
|
Not Promoted |
0.17 |
0.56 |
a. What is the probability that a randomly selected officer is promoted?
b. What is the probability that a randomly selected officer is female and is not promoted?
c. What is the probability that a randomly selected officer is promoted given a female officer?
d. What is the probability that a randomly selected officer is promoted given a male officer?
e. Are the events "being promoted" and "being female" mutually exclusivet? Are they independent? Please justify your answer to receive a credit.
PLEASE ANSWER EITHER ONE OF THE FOLLOWING TWO QUESTIONS
5. A somewhat absent-minded hiker forgets to bring her/his insect repellent on 30% of her/his hikes. The probability of being bitten is 90% if s/he forgets the repellent, and 20% if s/he uses the repellent.
a. What is the probability that she will be bitten?
b. What is the probability that she forgot her repellent given that she was bitten?
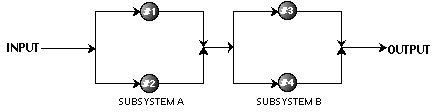
5. Consider the following system of components connected as in the accompanying pictures. The probability of failure for components in the system is 0.1. Assume components operate independently of each other.
a. Find the probability that the system will fail to operates properly.
b. Find the probability that at least one of the subsystems will fail.