---

Most important element in the solution of the probability and statistics problems is the nonuniqueness of the solution method. The following graphical and tabular techniques are aimed to help to understand the problem better:

I. Straight forward logical set up,

II. Tables representations,

III. Venn diagrams,

IV. Trees.

Straight forward logical set up gives the fastest solution of the problem. But it requires a deep understanding of the definitions, concepts, theorems, and formulas. Last three techniques help to eliminate this difficulty. These techniques help to develop a logical and systematic thinking process on the solution of the problem. Direct, blind-folded use of formulas might endanger logical thinking and generally leads to an incorrect solution of a problem. Whatever technique one prefers, the basic steps are;

(i) Define the experiment,

(ii) Define the sample space (simple outcomes of the experiment)

(iii) Define the events that are given in the problem by using capital letters

(iv) For compound events use the set notation that we discussed before

(v) Write down the event that we would like to find the chance of occurrence on

(vi) Select the formula that will give us that probability given the information on the events you defined in (iii) & (iv).

(vii) Use your intuition and prior knowledge on the result and interpret that number. Does it make any sense? Is it what you expected?, If not, did you carry out your calculations correctly?

Example: A softball team has three pitchers, A, B, and C, with winning percentages of 0.4, 0.6, and 0.8, respectively. These pitchers pitch with frequency 2,3, and 5 out of every 10 games, respectively.

(a) What is the probability that the team will win the game?

(b) Suppose that the team won the game what is the probability that A pitched the game?

What is the experiment? : Each game in this problem is the experiment

What are the possible outcomes of the experiment? : First of all A may pitch the game or B may pitch the game or C may pitch the game. So let us label each one of these simple events

A = the event that A will pitch the game

B = the event that B will pitch the game

C = the event that C will pitch the game

Secondly, the team may win the game or lose the game, so let us label these outcomes

W = the event that the team will win the game

L = the event that the team will lose the game

What is the relation between the events? That is are they disjoint (mutually exclusive) or independent?

Since the team can not win and lose the game at the same time W and L are disjoint (mutually exclusive).

If we assume that only one pitcher pitches the whole game A, B, and C are also disjoint (mutually exclusive).

The questions that you must have at this point are the following:

Are the events A, W disjoint (mutually exclusive)? If yes, what does it say for the pitcher A?

Are the events B, L disjoint (mutually exclusive)? If yes, what does it say for the pitcher B?

Are the events A, W independent? If yes, what does it say for the pitcher A?

Are the events B, L dependent? If yes, what does it say for the pitcher B?

The translation of the mathematics notation to the daily language plays an important role in understanding and solving problems related with probability. The following table shows the translation of these languages from one another.

Now, fill out the following table for the A and W being independent.

What are the numbers that are given in the statement of the problem?

First of all the problem says A has a winning average 0.4. So A will win 40% of the games. But for A to win the game it should play the game as a pitcher. In other words A will win the game given that he plays the game. Therefore,

P(W | A) = 0.40

P(W | B) = 0.60

P(W | C) = 0.80.

Since these pitchers pitch with frequency 2, 3, and 5 out of every 10 games, respectively;

P(A) = 0.20

P(B) = 0.30

P(C) = 0.50.

The first part of the problem is asking for P(W). What is the difference between P(W) and any one of the following probabilities P(W | A), P(W | B), and P(W | C)?

The second part of the problem is asking for P(A | W). What is the difference between P(W | A) = 0.40 and P(A | W)?

What do you think that P(A | W) + P(B | W) + P(C | W) will be equal to?

Given the information on P(A), P(B), P(C), P(W | A), P(W | B), and P(W | C), Do you expect that P(A | W) will be greater than P(C | W) ? Why or why not?

Note that the components that will affect the P(A | W) are (i) A should play, that is P(A) and (ii) the team should win, that is P(W | A).

Now, we will solve the problem by using the 4 techniques that we introduced above.

Solution I. To find out P(W), one might use the following logical steps:

(i) In which cases the team will win the game. The team will win the game when A pitches, or B pitches, or C pitches. Therefore

"The team wins the game" = "A pitches and the team wins"

or "B pitches and the team wins"

or "C pitches and the team wins".

By using our notation;

W = (A and W) or (B and W) or (C and W)

Are the events AW, BW, CW disjoint (mutually exclusive)? Justify your answer.

P(W) = P(AW or BW or CW) = P(AW) + P(BW) + P(CW) (Why?)

Do we know the value of P(AW), P(BW), and P(CW)?

Can we find P(AW), P(BW), and P(CW) given the information on P(A), P(B), P(C),

P(W | A), P(W | B), and P(W | C)?

By using the multiplication rule (definition of the conditional probability), we end up with

P(AW) = P(W | A) P(A) = 0.40 x 0.20 = 0.08

P(BW) = P(W | B) P(B) = 0.60 x 0.30 = 0.18

P(CW) = P(W | C) P(C) = 0.80 x 0.50 = 0.40

Note that the multiplication rule on P(AW) can be used also as follows:

P(AW) = P(A | W)P(W). Why we did not use this form?

Is P(AW) = P(A | W)P(W) = P(W | A) P(A) ? Justify your answer.

Therefore, P(W) = P(AW) + P(BW) + P(CW)

= P(W | A)P(A) + P(W | B) P(B) + P(W | C) P(C)

= 0.08 + 0.18 + 0.40 = 0.66

The second part of the problem is asking for P(A | W). By using the definition of the conditional probability, we end up with

How did we get the second part of the above formula?

Therefore,

P(A | W) = 0.121. Similarly P(B | W) = 0.273, and P(C | W) = 0.606.

We are going to interpret these results after we discuss all of the solution techniques.

Solution II. Tables. The information that is given in the problem can be represented by using a table. In this table the rows will show the result of the game, and the columns will show who pitches the game. The elements in the table will provide the probability that the corresponding row and column elements occur together.

Note that this table gives us some important formulas such as

P(AandW) + P(BandW) + P(CandW) = P(W)

P(AandW) + P(AandW) + P(AandW) = P(W)

If the conditional probabilities are available table can be modified by using the multiplication rule as follows;

Now, let us fill out the table with the probabilities that are given

Fill out the rest of the table, and find P(W) and P(A | W).

Solution III. This time we will use a Venn diagram. Each region on the diagram will correspond to a relevant event.

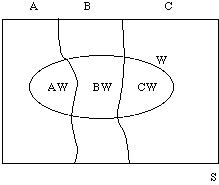
Since the probability is a special type of measure, just like the area of each piece on the graph, same type of argument that is given in the solution I can be used to answer to the question.

Solution IV. Trees. When we analyze an experiment that takes place in a sequence of steps, we often find it convenient to represent the sample space by the set of all paths through the tree. A probability measure is assigned by considering the conditional probabilities appropriate for the outcome of the any step, given all previous outcomes. These weights are assigned at the appropriate branches of the tree, and then the weights for a path through the tree is the product of the branch weights along the path. In our experiment first of all one of the pitchers should pitch the game then the team either will win or lose. Therefore corresponding tree can be constructed as follows:

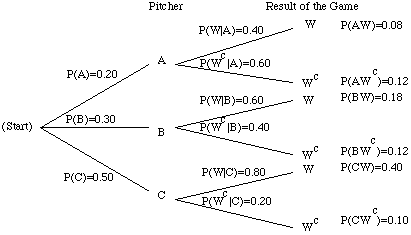
Mark the paths on the tree where the team ends up winning the game. By using these paths write down the formula for finding P(W)

Find the probability that the team will win the game by using the above formula

Suppose that the team wins the game. Given this information some of the branches of the tree will be chopped off.

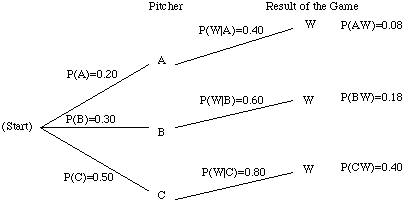
Write down the formula to find P(A | W)

Use the formula to find P(A | W)

Our original tree gave us the probabilities for the result of the game given the pitcher. The i.inverse probabilities,; that is probabilities for the pitcher given the result of the game are called Bayes probabilities. These inverse probabilities can also be obtained by simply constructing the three for the two-stage experiment carried out in reverse order.

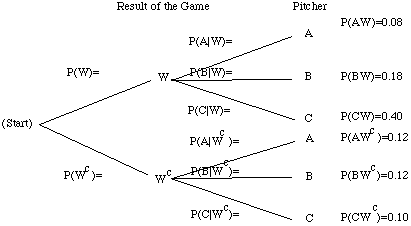
Fill out the rest of the above reverse tree by using P(W) and P(W) that you have already found.

In this part we will try to interpret the results that we got. Note that if the pitcher C pitched all the games the probability of winning would be 0.80. The probability of winning reduces to 0.66 since all the games are not pitched by C and all the pitcher are not equally good.

If all the pitchers are equally good, say with the winning percentage 0.80, what would be the probability that the team will win?

The winning percentages for the pitchers A, B, and C are 0.40, 0.60, and 0.80 respectively. And A, B, C pitches 20%, 30%, and 50% of the games.

Given the winning percentages for each pitcher, is it reasonable if A, B, and C pitches 50%, 30%, and 20% of the games?

If the team is winning the probability that A is pitching the game is 0.121. If all the pitchers were equally good, that is winning is independent to the whether A is pitching or not, what would this probability be equal to?

What type of relation do you expect between P(C | W) and P(C)? (P(C | W) > P(C) or

P(C | W) < P(C) or P(C | W) = P(C))