&nbsp;

http://www.bea.doc.gov/bea/regional/reis/

Regional Economic Information System

Minnesota Workforce Center

http://www.mnwfc.org/lmi/lmi4.htm

County Business Patterns

http://fisher.lib.virginia.edu/cbp/

Environmental Protection Agency

Environmental data – www.epa.gov

Counties and Cities in West Central Minnesota

Please circle the group that you will be working with.

Region 1

Becker (7) – Audubon, Callaway, Detroit Lakes, Frazee, Lake Park, Ogema, Wolf Lake

Clay (11) – Barnesville, Comstock, Dilworth, Felton, Georgetown, Glyndon, Hawley, Hitterdal, Moorhead, Sabin, Ulen

Douglas (11) – Alexandria, Brandon, Carlos, Evansville, Forada, Garfield, Kensington, Millerville, Miltona, Nelson, Osakis

Region 2

Grant (7) – Ashby, Barrett, Elbow Lake, Herman, Hoffman, Norcross, Wendell

Otter Tail (22) – Battle Lake, Bluffton, Clitherall, Dalton, Deer Creek, Dent, Elizabeth, Erhard, Fergus Falls, Henning, New York Mills, Ottertail, Parkers Prairie, Pelican Rapids, Perham, Richville, (Rothsay)*, Underwood, Urbank, Vergas, Vining, Wadena

Region 3

Pope (10) – Brooten, Cyrus, Farwell, Glenwood, Long Beach, Lowry, Sedan, Starbuck, Villard, Westport

Stevens (5) – Alberta, Chokio, Donnelly, Hancock, Morris

Traverse (4) – Browns Valley, Dumont, Tintah, Wheaton

Wilkin (9) – Breckenridge, Campbell, Doran, Foxhome, Kent, Nashua, Rothsay*, Tenney, Wolverton

West Central Minnesota has a total of 85 unique cities in 9 counties.

* The city of Rothsay overlays two counties, Otter Tail and Wilkin. Students in Region 3, covering Wilkin County, will be responsible for getting the data for the entire city. To do this you must combine the data from both counties to get an accurate picture of the entire city.

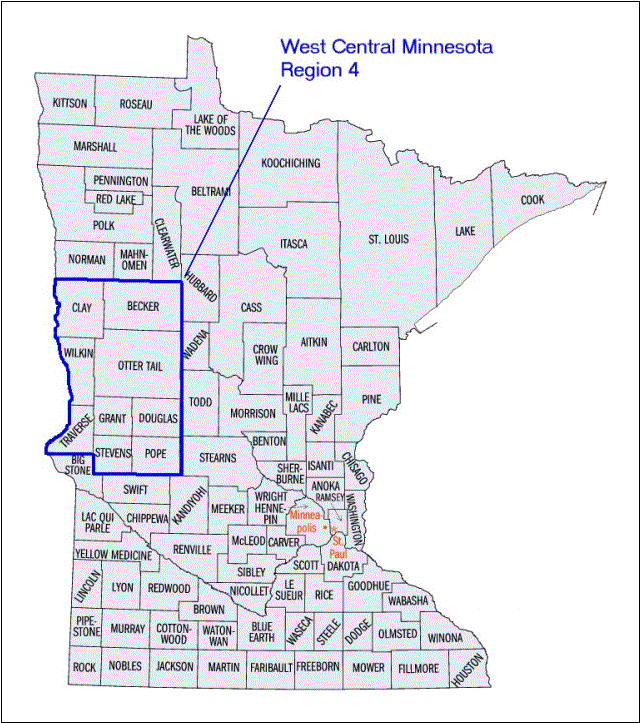Map of Minnesota Counties

Chapter 1: Looking at Data – Distributions

Chapter Objectives (course)

Construct and interpret graphical displays of the distribution of a dataset.
Compute and interpret appropriate numerical summaries of a distribution.
Use the normal distribution to describe important features of a dataset

Section 1.1. Displaying Distributions with Graphs

Technique:
Stemplots, Histograms, Time plots.

Objective (civic learning):

Data Information:

http://factfinder.census.gov

Warm-up Activity

1. Produce a histogram of the Age variable for each City in your region.

Use General Characteristics: Population and Housing for 2000 using http://factfinder.census.gov .
Select the category you want to use (General Characteristics: Population and Housing for 2000)
Select the type of district (City or Town)
Select the state (Minnesota)
Select the City
Use the percentages for the histogram. On the x-axis, use the different age groups such as: Under 5 years, 5-9 years, --- , 85 years and over and on the y-axis, use the number of individuals appeared as the percentage of the total population.

Main Activity

1. Produce a stemplot for Liquor Sales that includes all of the Counties in West Central Minnesota: Becker County, Clay County, Douglas County, Grant County, Otter Tail County, Pope County, Stevens County, Traverse County, and Wilkin County using the variable Liquor Sales Per Capita for 1996 using the web page http://www.mnplan.state.mn.us/datanetweb/ .

Select the category Statistics Abuse Monitoring System
Select the type of district (County)
Select your county
Under County Ranking select Liquor Sales Per Capita for 1996.
Start your stemplot at 0 and end it with 500 rounding to the nearest whole number (Example: 99.85 would round to 100).

2. Produce a histogram of the Age variable for each County in your region using the General Characteristics: Population and Housing for 2000 at http://factfinder.census.gov .

Select the category you want to use (General Characteristics: Population and Housing for 2000)
Select the type of district (County)
Select the state (Minnesota)
On the x-axis, use the different age groups such as: Under 5 years, 5-9 years, --- , 85 years and over and on the y-axis, use the number of individuals or the percentage of the population.

3. Produce a time plot for the Population for each County in your region using the web page http://www.mnplan.state.mn.us/datanetweb/ and go to Census 2000 SF1 Data and under Population Profiles
a. Select Population in 1970, 1980, 1990, 2000

b. Select Report

c. For the Choose an Area, choose County, and then hit Enter choice

d. Select your county and make a time plot for the population from 1970 to 2000.

Section 1.2. Describing Distributions with Numbers

Technique:

Mean, Median, Quartiles, Interquartile range, The five-number summary and boxplots, Standard deviation.

Objective (civic learning):

Data Information:

http://factfinder.census.gov

Warm-up Activity

1. Calculate the mean, median, mode and standard deviation of the Median Age for all of the Cities in your region.

Use the category General Characteristics: Population and Housing for 2000 using http://factfinder.census.gov .
Select the category you want to use (General Characteristics: Population and Housing for 2000)
Select the type of district (City or Town)
Select the state (Minnesota).
Select the county your cities are in.
Select one of the cities, note the Median Age.
Repeat these steps for all cities.

Main Activity

1. Calculate the mean, median, mode and standard deviation of Median Age for all of the Counties in West Central Minnesota (not just those in your region).

Use the category General Characteristics: Population and Housing for 2000 using http://factfinder.census.gov .
Select the category you want to use (General Characteristics: Population and Housing for 2000)
Select the type of district (County)
Select the state (Minnesota).
Select one of your counties, note the Median Age.
Repeat these steps for Age for 1990

2. A. Calculate the interquartile range of the variable Liquor Sales Per Capita for 1996 for the following Counties in Minnesota: Becker County, Clay County, Douglas County, Grant County, Otter Tail County, Pope County, Stevens County, Traverse County, and Wilkin County using http://www.mnplan.state.mn.us/datanetweb/

Select the category Substance Abuse Monitoring System
Select the type of district (County)
Select your county
Under County Ranking select the variable Liquor Sales Per Capita for 1996 and for the Liquor Sales Per Capita, round to the nearest whole number.

2. B. From 2.A., are there are any possible Outliers for Liquor Sales Per Capita?

2. C. From 2.A., calculate the Standard Deviation for Liquor Sales Per Capita.

3. Produce a Boxplot of the variable Liquor Sales Per Capita for 1996 that includes the following Counties in Minnesota: Becker County, Clay County, Douglas County, Grant County, Otter Tail County, Pope County, Stevens County, Traverse County, and Wilkin County using http://www.mnplan.state.mn.us/datanetweb/

Select the category Substance Abuse Monitoring System
Select the type of district (County)
Select your county
Under County Ranking select the variable Liquor Sales Per Capita for 1996 and for the Liquor Sales Per Capita, round to the nearest whole number.

Section 1.3. The Normal Distributions

Technique:

Density curves, Normal Distributions, The 68-95-99.7 rule, Standardizing observations, Normal quartile plots, Normal quantile plots, Density estimation.

Objective (civic learning):

Data Information:

Warm-up Activity

The variable of interest for this problem is the Average Household Size. This activity will look all Counties in West Central Minnesota. To get the correct data, use the following steps:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF1 Data
Under Household Profiles, select Population and Average Household Size by Race, click Report
Under Choose an Area, select County
Select All Races

1. Calculate the mean and standard deviation of the Average Household Size in counties across West Central Minnesota.

2. What is the area under the standard normal curve to the left of the first quartile? Use this to find the value of the first quartile for a standard normal distribution. Find the third quartile similarly.

3. Compute the z-score for each of the counties.

4. What is the value of the interquartile range for the standard normal distribution?

5.A. What proportion of counties are within 1 standard deviation of the mean?

5.B. What proportion of counties are within 2 standard deviations of the mean?

5.C. What proportion of counties are within 3 standard deviations of the mean?

6. Compare the proportions found in #5(A,B,C) with the 68-95-99.7 rule.

7. What is the proportion of counties with an Average Household Size less than 3?

Main Activity

The variable of interest for this problem is the Average Household Size. This activity will look all Counties in West Central Minnesota. To get the correct data, use the following steps:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF1 Data
Under Household Profiles, select Population and Average Household Size by Race, click Report
Under Choose an Area, select Minor Civil Division
Select the county that the city is in
Select the city
Select All Races

1. Calculate the mean and standard deviation of the Average Household Size in cities across West Central Minnesota.

2. Compute the z-score for each of the cities.

3.A. What proportion of cities are within 1 standard deviation of the mean?

3.B. What proportion of cities are within 2 standard deviations of the mean?

3.C. What proportion of cities are within 3 standard deviations of the mean?

4. Compare the proportions found in #3(A,B,C) with the 68-95-99.7 rule.

5. What is the proportion of cities with an Average Household Size less than 3?

Chapter 2: Looking at Data - Relationships

Chapter Objectives (course):

Construct and interpret graphical displays of the relationship between two continuous or categorical variables.
Compute and interpret appropriate numerical summaries of a relationship.
Use the tools of linear regression and correlation to describe important features of a relationship.

Section 2.1. Scatterplots

Technique:

Scatterplots, Adding categorical variables to scatterplots, Scatterplot smoothers.

Objective (civic learning):

Data Information:

Warm-up Activity

1.A. For each City in your region, produce a scatterplot for the variable Percentage of Population age 25+ with a Bachelors Degree (or higher) against Median Household Income. Be aware of the scale on each axis. What is the incremental unit (10/100/10,000)?

For Bachelors Degree:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Social Characteristics, select Educational Attainment, click Report
Under Choose an Area, select City
Select the City
Note the percentage with Bachelors Degree (or higher) and repeat for all cities in your region.

For Median Household Income:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Economic Characteristics, select Income, click Report
Under Choose an Area, select City
Select the City
Note the Median Household Income and repeat for all cities in your region.

1.B. Describe the relationship that you see.

Main Activity

1.A. For each City in your region, produce a scatterplot for the variable Population in 2000 against Median Household Income.

For Population:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF1 Data
Under Population Profiles, select Population in 1970, 1980, 1990, 2000
Under Choose an Area, select Minor Civil Division
Select the County in which the City resides
Note the population of the city. Repeat for all cities in your region.

For Median Household Income:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Economic Characteristics, select Income, click Report
Under Choose an Area, select City
Select the City
Note the Median Household Income and repeat for all cities in your region.

1.B. Describe the relationship that you see.

Section 2.2. Correlation

Technique:

Correlation r.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

1. Produce a graph and calculate the correlation r for the two variables Alcohol Use (12^thgrade) and Driving Under the Influence of Alcohol or Drugs (12^thgrade) for the following counties in Minnesota: Becker County, Clay County, Douglas County, Grant County, Otter Tail County, Pope County, Stevens County, Traverse County, and Wilkin County. To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select the category Children’s Report Card
Select the type of district (County)
Select your county
Under the category County Ranking for Selected Indicator, select the year (1999) and select either one of the variables (Alcohol Use (12^thgrade) or Driving Under the Influence of Alcohol or Drugs (12^thgrade)).

A. Is there a correlation?
B. If so, describe the correlation (What direction and strength?).

Section 2.3. Least-Squares Regression

Technique:

Fitting a line to data, Prediction, Least-squares regression, r²

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

1. Using all of the Cities in your region, make a scatterplot of Median Home Value against Median Household Income. Describe the form and direction of the relationship.

2. Construct a Least-Squares Regression Line for each county in your region.

To get the correct data, use the following steps:

Part 1: Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Housing Characteristics, select Value
Select City
Gather data of the Median Value(dollars)
Repeat for all the cities in the counties of your region.
Part 2: Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Economic Characteristics, select Income in 1999
Select City
Look at the Median Household Income (dollars)
Repeat for all the cities in the counties of your region.

3. Interpret the coefficient and the constant.

4. Predict the income a person must have to afford a $100,000 home in your region.

Section 2.4. Cautions about Regression and Correlation

Technique:

Residuals, Outliers and influential observations.

Objective (civic learning):

Data Information:

http://factfinder.census.gov

Warm-up Activity

1. Construct a Least-Squares Regression Line for the State of Minnesota for the variable Total Part 1 Offenses Crimes Reported from 1985 to 1999 using http://www.mnplan.state.mn.us/datanetweb/. To get the correct data, use the following steps:

a. Go to the web site and select the category Justice Profiles

b. Select the category Reported Crimes

c. Select County and highlight all of the years (You can do this by clicking and holding down the shift key).

d. Use the variable Total Part 1 Offenses and put the Total Part 1 Offenses on the y-axis and the years from 1985 to 1999 on the x-axis.

e. Determine a Least-Squares Regression Line of Total Part 1 Offenses Crimes Reported against Time

A. Compute the residuals and make a plot of the residuals against x. Describe carefully the pattern displayed by the residuals.

Main Activity

1. Construct a Least-Squares Regression Line for each County in your region for the variable Total Part 1 Offenses Crimes Reported from 1985 to 1999 using http://www.mnplan.state.mn.us/datanetweb/ . To get the correct data, use the following steps:

Go to the web site and select the category Justice Profiles
Select the category Reported Crimes
Select County
Select your county and highlight all of the years (You can do this by clicking and holding down the shift key).
Use the variable Total Part 1 Offenses and put the Total Part 1 Offenses on the y-axis and the years from 1985 to 1999 on the x-axis.
Determine a Least-Squares Regression Line of Total Part 1 Offenses Crimes Reported against Time

A. Compute the residuals and make a plot of the residuals against x. Describe carefully the pattern displayed by the residuals.

Section 2.5. An Application: Exponential Growth and World Oil Production

Technique:

The nature of exponential growth, The logarithm transformation

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

Section 2.6. Relations in Categorical Data

Technique:

Marginal distributions, Conditional distributions, Simpson’s paradox, The perils of aggregation.

Objective (civic learning):

Data Information:

Warm-up Activity

1. A. Find the marginal distribution of Age for the State of Minnesota (in percent) and make a bar graph of the distribution. To do the warm-up activity, you must first go to the web site http://factfinder.census.gov. To get the correct data, use the following steps:

Under Show Me, select Population, Age, and Sex in the Census 2000 Geographic Comparison Tables for the variable
Select the type of district (State -- County)
Select the state (Minnesota) and press Go.

1. B. Find the conditional distribution of age for the state of Minnesota (in percent) and make a bar graph of this distribution.

1. C. Briefly describe the most important difference between the two age distributions.

Main Activity

1. Find the marginal distribution of Age for each County in your region (in percent) and make a bar graph of the distribution. To do this activity, you must first go to the web site http://factfinder.census.gov. To get the correct data, use the following steps:

Under Show Me, select Population, Age, and Sex in the Census 2000 Geographic Comparison Tables for the variable
Select the type of district (State -- County)
Select the state (Minnesota) and press Go.

B. Find the conditional distribution of age for your county (in percent) and make a bar graph of this distribution.

C. Briefly describe the most important difference between the two age distributions.

Section 2.7. The Question of Causation

Technique:

Causation, Common response, Confounding.

Objective (civic learning):

Data Information:

Main Activity

1.A. For each City in your region, produce a scatterplot for the variable Educational Attainment against Median Household Income.

For Educational Attainment data:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Social Characteristics, select Educational Attainment
Under Choose an Area, select Minor Civil Division
Select the County in which the City resides
Note the population of the city. Repeat for all cities in your region.

For Median Household Income data:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Economic Characteristics, select Income, click Report
Under Choose an Area, select City
Select the City
Note the Median Household Income and repeat for all cities in your region.

1.B. Describe the relationship that you see between Educational Attainment and Median Household Income. Does a high income cause a high level educational attainment or does educational attainment cause a higher income?

2.A. For each City in your region, produce a scatterplot for the variable Median Age against Median Household Income.

For Median Age data:

Use General Characteristics: Population and Housing for 2000 using http://factfinder.census.gov .
Select the category you want to use (General Characteristics: Population and Housing for 2000)
Select the type of district (City or Town)
Select the state (Minnesota)
Select the City
Note the median age and repeat for all cities in your region.

For Median Household Income data:

Go to the web site, http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF3 Data
Under Economic Characteristics, select Income, click Report
Under Choose an Area, select City
Select the City
Note the Median Household Income and repeat for all cities in your region.

2.B. Describe the relationship that you see between Age and Household Income. Does this mean that as you get older you will make more money? Is this guaranteed? Explain your response to these questions.

Chapter 3: Producing Data

Chapter Objectives (course):

Understand benefits of random sampling.
Understand basic principles of sampling designs.
Understand basic principles of experimental design.
Understand distinction between population and sample.

Section 3.1. First Steps

Technique:

Sampling, Experiments.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

Extension

Section 3.2. Design of Experiments

Technique:

Comparative experiments, Randomization, Matched pairs design, Block designs.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

1. Results from polls and other statistical studies reported in a newspaper or magazines often emphasize the point that the samples were randomly selected. Why the emphasis on randomization? Couldn't a good investigator do better by carefully choosing respondents to a poll so that various interest groups were represented? Perhaps, but samples selected without objective randomization tend to favor one part of the population over another. For example, polls conducted by sports writers tend to favor the opinions of sport fans. This leaning toward one side of the issue is called sampling bias. In the long run, random samples seem to do a good job of producing samples that fairly represent the population. In other words, randomization reduces sampling bias.

Question: How do random samples compare to subjective samples in terms of sampling bias?

Section 3.3. Sampling Design

Technique:

Simple random samples, Stratified samples, Multistage samples.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

1. This is the data that we have obtained from one of our courses on "Random Fortunes".

Student Number	Initial Guess	Subjective (Judgmental) Sample Average	Random Sample Average
1	16	14.4	10.6
2	10	10.8	7
3	18	14	6
4	15	15.4	7
5	18	10	5
6	12	10	4
7	10	10.8	4.8
8	15	10.6	3.2
9	12	12.6	5.8
10	13	12.2	7.9
11	12	14	5.6
12	12	10.5	9.2
13	12	12.8	7
14	9	9.4	5.7
15	18	14.4	7.6
16	16	11.4	8.2
17	18	18	10.2
18	10	10.2	8.2
19	12	9.4	6.6
20	10	10.2	8.4

Table X:

A. First look at guesses and the averages of subjective samples of 5 from each member of the class. Display the two sets of data on separate stemplots or dot plots. Comment upon the shape of these distributions and where they center. Why is the center an important point to consider?

a) Look at the averages from the random samples of size 5 and construct a stemplot or a dot plot. How does this plot compare with the plots of the guessed values and the averages from the subjective samples in terms of center? In terms of spread.

b) From the data the instructor has provided for the whole class, calculate the mean of the sample averages for the subjective samples and for the random samples. How do the centers of the distributions of means compare?

c) Calculate the standard deviation of the averages for the subjective and for the random samples. How do the spreads of the distributions of means compare?

d) Having studied two types of sampling, subjective and random, which method do you think is doing the better job? Why?

Section 3.4. Toward Statistical Inference

Technique:

Sampling variability, Sampling distributions, Capture-recapture sampling.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

Chapter 4: Probability and Inference

Chapter Objectives (course):

Phrase an inference about a population by making a jump from sample to population and then to give a measure of reliability for the inference.
Understand basic concepts of probability
Identify random variables and find probabilities of specific numerical outcomes
Find and interpret mean and variance of random variables

Section 4.1. Randomness

Technique: Randomness, The uses of probability.

Objective (civic learning):

Data Information:

Warm-up Activity

Section 4. Probability Models

Technique:

Samples spaces, Intuitive probability, Finite number of outcomes, Equally likely outcomes.

Objective (civic learning):

Data Information:

4.2.1: http://factfinder.census.gov

Warm-up Activity

1. What is the probability of a male between 25 and 44 years of Age residing in the State of Minnesota (in percent)? To get the correct data, use the following steps:

Go the web site http://factfinder.census.gov .
Under Show Me, select Population, Age, and Sex in the Census 2000 Geographic Comparison Tables for the variable
Select the type of district (State -- County)
Select the state (Minnesota) and press Go.

2. What is the probability of an American Indian and Alaskan Native male between 25 years old to 44 years old for Minnesota (in percent) using the tables below.

Main Activity

1. What is the probability of a male between 25 and 44 years of Age residing in each of the Counties in your region (in percent)? To get the correct data, use the following steps:

a. Go the web site http://factfinder.census.gov .

b. Under Show Me, select Population, Age, and Sex in the Census 2000 Geographic Comparison Tables for the variable

c. Select the type of district (State -- County)

d. Select the state (Minnesota) and press Go.

2. What is the probability of an American Indian and Alaskan Native male between 25 years old to 44 years old for your county (in percent) using the tables below.

American Indian and Alaska Native
Geographic Area	Percent
Minnesota	1.1
Becker County	7.5
Clay County	1.4
Douglas County	0.2
Grant County	0.2
Ottertail County	0.3
Pope County	0.5
Stevens County	0.2
Traverse County	2.8
Wilkin County	0.4

Table: American Indian and Alaska Native in percent.

Geographic Area	Total Population	Percent of total population					Median age (years)	Males per 100 females
Geographic Area	Total Population	Under 18 years	18 to 24 years	25 to 44 years	45 to 64 years	65 years and over	Median age (years)	All ages	18 years and over
Minnesota	4,919,479	26.2	9.6	30.4	21.8	12.1	35.4	98.1	95.6
Becker County	30,000	26.6	7.1	24.9	24.9	16.4	39.4	99.4	97.8
Clay County	51,229	25.0	17.1	25.7	19.3	12.9	32.3	93.7	89.1
Douglas County	32,821	24.0	9.2	25.0	23.8	17.9	39.7	99.0	96.9
Grant County	6,289	23.9	6.9	23.1	23.2	22.9	42.5	94.5	94.3
Otter Tail County	57,159	24.9	7.2	24.2	24.7	19.0	41.1	100.4	97.8
Pope County	11,236	24.8	6.7	23.1	23.8	21.5	42.1	96.9	92.9
Stevens County	10,053	21.6	20.8	21.6	19.0	17.0	33.9	93.9	91.0
Traverse County	4,134	25.3	5.6	21.7	21.2	26.2	42.9	96.7	93.8
Wilkin County	7,138	27.8	7.0	27.7	21.5	16.1	38.1	95.3	96.1

Table: Total population and percent of total population for the geographic area.

Section 4.3. Random Variables

Technique:

Discrete random variables, Continuous random variables, Normal distributions as probability distributions.

Objective (civic learning):

Data Information:

4.3.1: http://factfinder.census.gov

Warm-up Activity

Main Activity

1. Using the table below.

A. For Minnesota, what is the probability that a Householder which Moved into their unit between 1980 to 1989 still lives in their unit at 1999 to March 2000?

B. Check that this is a legitimate discrete probability distribution.

C. Find P(X >= 1980 to 1989).

D. Find P(X > 1980 to 1989).

Year Householder Moved into Unit (Minnesota)

Years	Probability
1999 to March 2000	0.037
1995 to 1998	0.044
1990 to 1994	0.062
1980 to 1989	0.075
1970 to 1979	0.090
1969 or earlier	0.100

Table: The year the householder moved into the unit for the state of Minnesota.

Section 4.4. Means and Variances of Random Variables

Technique:

The mean of a random variable, Statistical estimation and the law of large number, The variance of a random variable.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

Section 4.5. General Probability Rules

Technique:

Conditional probability, Tree diagrams, Decision analysis

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

1. Use the table below for the following questions about the State of Minnesota for 1999:

A. What is the probability that a randomly selected suicide victim is less than 20 years old?

B. What is the probability that a randomly selected motor vehicle injury is under 20 years of age?

C. What is the conditional probability that a fatal injury occurred, given that the individual was under 20 years of age?

State of Minnesota: Morbidity and Utilization

Description	<20 Years	20+ Years
Description	Number	Number
Fatal Injuries	203	1,560
Motor Vehicle Injuries	121	512
Suicide	39	399

Table:  Fatal Injury, Motor Vehicle, and Suicide cases for 1999 in the state of Minnesota.

Chapter 5: From Probability to Inference

Chapter Objectives (course):

5.1 Counts and Proportions

Understanding what a binomial experiment is
Checking the assumptions of a binomial experiment
How to use binomial tables to find probabilities
Finding mean and variance of counts under binomial experiment
Understanding the difference between sample and population proportion
Understanding the connection between counts and sample proportions
Finding sample proportion probabilities by using binomial tables
Finding the mean and variance of sample proportions
Finding count and sample proportion probabilities by using normal approximation

5.2 Sample Means

Understanding the difference between population mean and sample mean
Finding the mean and standard deviation of the sample mean
Determining sampling distribution of sample mean for normal and nonnormal populations

Section 5.1. Sampling Distributions for Counts and Proportions

Technique:

The binomial distributions for sample counts, Binomial distributions in statistical sampling, Finding binomial probabilities, Binomial mean and standard deviation, Sample proportions, Normal approximation for counts and proportions.

Objective (civic learning):

Data Information:

Warm-up Activity

1. Use the information from below about Arrests and Apprehensions in the State of Minnesota:

Arrests and Apprehensions in the state of Minnesota for 1999:

Population in 1999 = 4,919,479

Arrests & Apprehensions in 1999 = 269,395

Individuals involved in an Arrest or Apprehension in 1999 = 5.48%.

A. What are the mean and the standard deviation of the number X of arrests and apprehensions?

B. Use the normal approximation to find the probability that at least 269,395 arrests and apprehensions will occur.

C. What is the probability that more than 269,395 arrests and apprehensions will occur.
D. If the state of Minnesota grows to 5,500,000 by the year 2010, what is the probability that more than 301,400 arrests and apprehensions will occur.

Main Activity

1. For each County in your region:

A. What are the mean and the standard deviation of the number X of Arrests and Apprehensions?

B. Use the normal approximation to find the probability that at least the year 1999 arrests and apprehensions will occur.

C. What is the probability that more than the year 1999 arrests and apprehensions will occur.
D. If your county grows on average of 11.8% every ten years what will be the total population by the year 2010, what is the probability that more than the year 2010 arrests and apprehensions will occur.

To get the correct data for arrests and apprehensions, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/

b. Select Justice Profiles

c. Select Arrests and Apprehensions

d. Select the type of district (county)

e. Select 1999 for year and then select Total

f. Scroll to the bottom of the page and get the Grand Total/Total for arrests and apprehensions. The arrests and apprehensions have gone up on an average of 10.6% every ten years.

To get the correct data for the population, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Census 2000 SF1
Select Population Profiles
Select Population in 1970, 1980, 1990, and 2000
Select the type of district (county)
Select your county.

Section 5.2. The Sampling Distribution of a Sample Mean

Technique:

The mean and standard deviation of x, The sampling distribution of x, the central limit theorem, Weibull distributions.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

Section 5.3. Control Charts

Technique:

Statistical process control.

Objective (civic learning):

Data Information:

Warm-up Activity

Main Activity

Extension

Chapter 6: Introduction to Inference

Chapter Objectives (course):

6.1. Estimating with Confidence

Constructing a level C confidence interval for the population mean.
Understanding and interpreting confidence intervals
Determination of sample size for a given margin of error for the population mean.

6.2. Tests of Significance

Setting up null and alternative hypotheses
Finding and interpreting a P-value
Understanding tests with fixed significance level

6.3. Use and Abuse of Tests (excluding Power and Inference as Decision)

Finding the power of a test
Inference as decision

Section 6.1 . Estimating with Confidence

Technique:

Statistical confidence, Confidence Intervals, Confidence interval for a population mean, Choosing the sample size.

Objective (civic learning):

Data Information:

1. In the State of Minnesota, for Reported Burglary Crimes:

A. What is sigma x, the standard deviation of x-bar?
B. Give a 95% confidence interval for mu .

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/ .
Select Justice Profiles
Select Reported Crimes
Under Select Area, select State of Minnesota and
Highlight all of the years available (1985 to 1999)
Use the data under Burglary

1. In each County of your region, for Reported Burglary Crimes:

A. What is sigma x, the standard deviation of x-bar?
B. Give a 95% confidence interval for mu .

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/ .
Select Justice Profiles
Select Reported Crimes
Under Select Area, select County and then select your county
Highlight all of the years available (1985 to 1999)
Use the data under Burglary

Section 6.2 . Tests of Significance

Technique:

Stating hypothesis, Test statistics, P-values, Tests for a population mean, Two-sided significance tests and confidence intervals.

Objective (civic learning):

Data Information:

1. In the State of Minnesota, we want to compare the number of Burglaries Reported for 1990 and 1999 and see if there is a significant difference between the years:
A. State the appropriate H_o and H_a.
B. Carry out the test. Give the P-value, and then interpret the results in plain language.
C. Calculate the value z of the z test statistic.

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select State of Minnesota
Highlight all of the years available (1985 to 1999)
Use the data under Burglary

1. For each County in your region, we want to compare the number of Burglaries Reported for 1990 and 1999 and see if there is a significant difference between the years:
A. State the appropriate Ho and Ha.
B. Carry out the test. Give the P-value, and then interpret the results in plain language.
C. Calculate the value z of the z test statistic.

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select County
Select your county
Highlight all of the years available (1985 to 1999)
Use the data under Burglary

Section 6.3. Use and Abuse of Tests

Technique:

Objective (civic learning):

Data Information:

Section 6.4 . Power and Inference as a Decision

Technique:

Power, Increasing the power, Two types of error, Error probabilities

Objective (civic learning):

Data Information:

Chapter 7 : Inference for Distributions

Chapter Objectives (course):

7.1 Inference for the Mean of a Population Mean

Understanding t distribution and being able to use the t-tables
Setting up a confidence interval for m when s is unknown (assumptions)
Testing a hypothesis for m when s is unknown (assumptions) (P-value or fixed significance level)
Finding the power of t test
Making inference for nonnormal populations

7.2 Comparing two means

Section 7.1 . Inference for the Mean of a Population

Technique:

The t distributions, One-sample t confidence interval, One sample t test, Power of the t test, Sign test.

Objective (civic learning):

Data Information:

1. We will examine Reported Crimes for the State of Minnesota from 1985 to 1999:

A. Display the data with a stemplot and a normal quatntile plot. Describe the distribution.
B. Give a 95% confidence interval for the mean number of Grand Total crimes reported.

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select State of Minnesota
Highlight all of the years available (1985 to 1999)
Scroll down to the bottom of the page and you will see the Grand Total for Crimes Reported

1. We will examine Reported Crimes for each County in your region from 1985 to 1999:

A. Display the data with a stemplot and a normal quatntile plot. Describe the distribution.
B. Give a 95% confidence interval for the mean number of Grand Total crimes reported.

To get the correct data, use the following steps:

Go to the web page http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select County
Select your county
Highlight all of the years available (1985 to 1999)
Scroll down to the bottom of the page and you will see the Grand Total for Crimes Reported

Section 7.2 . Comparing Two Means

Technique:

The two-sample z statistic, Two-sample t procedures, Two-sample t significance test, Two-sample t confidence interval, Software approximation for the degrees of freedom, Pooled two-sample t procedures.

Objective (civic learning):

Data Information:

1. For Reported Crimes in the State of Minnesota from 1985 to 1999:

Group the years as the first five years, 1985 to 1992 and the second five years, 1993 to 1999. Compare the two five year periods to see if there is a significant difference between the mean amounts of Grand Total crimes reported. Does the data show a significant difference between the two means? Give the null and alternative hypothesizes, and calculate the two-sample t statistic. Obtain the P-value. State your practical conclusions.

To get the correct data, use the following steps:

Go the web page http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select State of Minnesota
Highlight or select all of the years available (1985 to 1999)
Scroll down to the bottom of the page and you will see the Grand Total for Crimes Reported

1. For Reported Crimes in each County of your region from 1985 to 1999:

To get the correct data, use the following steps:

Go to the web page http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select County
Select your county
Highlight or select all of the years available (1985 to 1999)
Scroll down to the bottom of the page and you will see the Grand Total for Crimes Reported

Section 7.3 . Optional Topics in Comparing Distributions

Technique:

Inference for population spread, The F test for equality of spread, The power of the two-sample t-test.

Objective (civic learning):

Data Information:

1. For the state of Minnesota from 1985 to 1999:

Group the years as the first five years, 1985 to 1992 and the second five years, 1993 to 1999. Compare the two five year periods to see if there is significant evidence of inequality between the standard deviations of the two populations of Grand Total crimes reported.
A. State the null and alternative hypothesis.

B. Calculate the F statistic. Between which two levels does the P-value lie?

To get the correct data, use the following steps:

Go to the web page http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select state of Minnesota
Highlight or select all of the years available (1985 to 1999)
Scroll down to the bottom of the page and you will see the Grand Total for Crimes Reported

1. For your county from 1985 to 1999:

B. Calculate the F statistic. Between which two levels does the P-value lie?

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Reported Crimes
Under Select Area, select County
Select your county
Highlight or select all of the years available (1985 to 1999)
Scroll down to the bottom of the page and you will see the Grand Total for Crimes Reported

Chapter 8: Inference for Proportions

Chapter Objectives (course):

8.1 Inference for a single proportion

Constructing confidence intervals for proportions
Determination of the Sample size
Carrying out significance tests for proportions

8.2 Comparing two proportions

Constructing confidence intervals for the difference between proportions
Carrying out significance tests for the difference between proportions

Section 8.1 . Inference for a Single Proportion

Technique:

Confidence interval for a single proportion, Significance test for a single proportion, Choosing a sample size.

Objective (civic learning):

Data Information:

Section 8.2 . Comparing Two Proportions

Technique:

Confidence intervals, Significance tests, Relative risk.

Objective (civic learning):

Data Information:

1. For Lung Cancer in the year 2000:

The state of Minnesota wants to know if there is a difference in Deaths versus Survival between Male and Female for lung cancer. Here are the data where n is the number of lung cancer cases diagnosed and X(Deaths) is the number of lung cancer deaths:

State of Minnesota

Population	n	X(Deaths)
Male	4,313	3,725
Female	3,061	2,582

Table X: Lung Cancer survival and deaths for males and females for the state of Minnesota.

A. Give the null and alternative hypotheses that are appropriate for this problem assuming that we have no prior information suggesting that one population would have a higher preference than the other.

B. Test the null hypothesis. Give the test statistic, the P-value, and summarize the results.
C. Give a 90% confidence interval for the difference in proportions.

1. For Lung Cancer in the year 2000:

Your county wants to know if there is a difference in Deaths versus Survival between Male and Female for lung cancer. Here are the data where n is the number of lung cancer cases diagnosed and X(Deaths) is the number of lung cancer deaths:

Becker County			Clay County
Population	n	X(Deaths)	Population	n	X(Deaths)
Male	38	27	Male	50	34
Female	31	28	Female	22	16
Douglas County			Grant County
Population	n	X(Deaths)	Population	n	X(Deaths)
Male	35	28	Male	5	5
Female	22	21	Female	3	3
Otter Tail County			Pope County
Population	n	X(Deaths)	Population	n	X(Deaths)
Male	64	51	Male	15	14
Female	44	30	Female	9	9
Stevens County			Traverse County
Population	n	X(Deaths)	Population	n	X(Deaths)
Male	11	8	Male	9	7
Female	7	2	Female	5	3
Wilkin County
Population	n	X(Deaths)
Male	11	9
Female	4	1

Table X: Lung Cancer survival and deaths cases for males and females by the demographic area.

B. Test the null hypothesis. Give the test statistic, the P-value, and summarize the results.
C. Give a 90% confidence interval for the difference in proportions.

Chapter 9 : Inference for Two-Way Tables

Chapter Objectives (course):

9.1 Inference for two-way tables

Two by two tables
Comparing many proportions
Analysis of general r by c tables.

Section 9.1 . Inference for Two-Way Tables

Technique:

The two-way table, Expected cell counts, The chi-square test, The chi-square test and the z test.

Objective (civic learning):

Data Information:

1. For Lung Cancer in the year 2000:

The state of Minnesota wants to know if there is a significant difference for Male and Female in Lung Cancer Deaths for the individuals Diagnosed for the year 2000. Use the data from below:

State of Minnesota

Lung Cancer Deaths for those Diagnosed	Gender
Lung Cancer Deaths for those Diagnosed	Male	Female
Yes	3,725	2,582
No	588	479

Table: Lung Cancer Deaths for those Diagnosed by Gender for the state of Minnesota.

A. Make a table that includes the following information for each group (Male or Female): total number of individuals diagnosed with Lung Cancer in the year 2000, the proportion of Lung Cancer Deaths for those Diagnosed, and the standard error for the proportion.

B. Perform the chi-square test for this two-way table. Give the test statistic, the degrees of freedom, the P-value, and your conclusion.

1. For Lung Cancer in the year 2000:

Your county wants to know if there is a significant difference for Male and Female in Lung Cancer Deaths for the individuals Diagnosed for the year 2000. Use the data from below:

Becker County			Clay County
Population	Male	Female	Population	Male	Female
Yes	27	28	Yes	34	16
No	11	3	No	16	6
Douglas County			Grant County
Population	Male	Female	Population	Male	Female
Yes	28	21	Yes	5	3
No	7	1	No	0	0
Otter Tail County			Pope County
Population	Male	Female	Population	Male	Female
Yes	51	30	Yes	14	9
No	13	14	No	1	0
Stevens County			Traverse County
Population	Male	Female	Population	Male	Female
Yes	8	2	Yes	7	3
No	3	5	No	2	2
Wilkin County
Population	Male	Female
Yes	9	1
No	2	3

Table X: Lung Cancer Deaths for those Diagnosed by Gender for the demographic area.

B. Perform the chi-square test for this two-way table. Give the test statistic, the degrees of freedom, the P-value, and your conclusion.

Section 9.2 . Formulas and Models for Two-Way Tables

Technique:

Computations, Computing conditional distributions, Computing expected cell counts, Computing the chi-square statistic, Testing independence for the second model.

Objective (civic learning):

Data Information:

1. For Cancer in the year 2000:

The state of Minnesota wants to know if there is a significant difference for Deaths Occurred for the Type of Cancer the individual has been diagnosed. Use the data from below:

The following table classifies the women by the Type of Cancer the individual has been diagnosed with and whether of not a death occurred from that type of cancer.

State of Minnesota

	Cancer Survival for Females
Type of Cancer	Dead	Survived
Breast	2176	7333
Colon & Rectum	1439	2163
Lung	2582	479
Other	6499	6679

Table X: Type of Cancer by Cancer Survival for Females for the state of Minnesota.

A. Carry out a complete analysis of the association between Cancer Deaths for Women and the Type of Cancer, including a description of the association and an assessment of its statistical significance. Summarize your conclusions.

1. For Cancer in the year 2000:

Your county wants to know if there is a significant difference for Deaths Occurred for the Type of Cancer the individual has been diagnosed.

Create a table that classifies the women by the Type of Cancer the individual has been diagnosed with and whether of not a death occurred from that type of cancer.

To get the correct data, use the following steps:

Go to the web page http://www.mnplan.state.mn.us/datanetweb/
Select Health Profiles
Under Select Area, select County
Select your county
Under Morbidity and Utilization, select Number of Cancer Cases Diagnosed by Major Site and Sex and hit enter choice
There you can get the types of cancer and how many women were diagnosed for each cancer type
Next, go back one page
Under Morbidity and Utilization, select Number of Cancer Deaths by Type of Cancer & Sex, hit enter choice
There you can get the types of cancer and how many women deaths occurred for each cancer type

A. Create a table that classifies the women by the Type of Cancer the individual has been diagnosed with and whether of not a death occurred from that type of cancer.

B. Carry out a complete analysis of the association between Cancer Deaths for Women and the Type of Cancer, including a description of the association and an assessment of its statistical significance. Summarize your conclusions.

Chapter 10: Inference for Regression

Chapter Objectives (course):

Understand simple linear regression model.
Understand confidence intervals for the slope parameter.
Understand hypothesis tests for the slope parameter.
Understand predictions for the response at a given level of the predictor variable

Section 10.1. Simple Linear Regression

Statistical model for linear regression, Estimating the regression parameters, Confidence intervals and significance tests, Confidence intervals for mean response, Prediction intervals.

Objective (civic learning):

Section 10.2. More Detail about Simple Linear Regression

Analysis of variance for regression, The ANOVA F, Calculations for regression inference, Preliminary calculations: Inference for slope and intercept, Confidence intervals for the mean response and prediction intervals for a future observation, and Inference for correlation.

Objective (civic learning):

Data Information:

1. A. Plot the Median Value of Homes (dollars) versus City and plot the Median Household Income (dollars) versus City. Describe the pattern. Are there any outliers or unusual towns?
B. Perform the regression analysis and summarize the results. Give the least-squares line and the results of the significance test for the slope.

C. Test the null hypothesis that the slope is zero and describe your conclusion.
D. Give a 95% confidence interval for the slope.

To get the correct data, use the following steps:

a. Go to the web page http://www.mnplan.state.mn.us/datanetweb/ .

b. Select Census 2000 SF3 Data

c. Under Housing Characteristics, select Value

d. Then select City and look at Median (dollars)

e. Repeat for all of the following cities: Audubon, Callaway, Detroit Lakes, Frazee, Lake Park, Ogema, Wolf Lake, Barnesville, Comstock, Dilworth, Felton, Georgetown, Glyndon, Hawley, Hitterdal, Moorhead, Sabin, Ulen, Alexandria, Brandon, Carlos, Evansville, Forada, Garfield, Kensington, Millerville, Miltona, Nelson, Osakis, Ashby, Barrett, Elbow Lake, Herman, Hoffman, Norcross, Wendell, Battle Lake, Bluffton, Clitherall, Dalton, Deer Creek, Dent, Elizabeth, Erhard, Fergus Falls, Henning, New York Mills, Ottertail, Parkers Prairie, Pelican Rapids, Perham, Richville, Rothsay*, Underwood, Urbank, Vergas, Vining, Wadena, Brooten, Cyrus, Farwell, Glenwood, Long Beach, Lowry, Sedan, Starbuck, Villard, Westport, Alberta, Chokio, Donnelly, Hancock, Morris, Browns Valley, Dumont, Tintah, Wheaton, Breckenridge, Campbell, Doran, Foxhome, Kent, Nashua, Rothsay*, Tenney, and Wolverton.

f.Then, go to the web page http://www.mnplan.state.mn.us/datanetweb/

g. Select Census 2000 SF3 Data

h. Under Economic Characteristics, select Income in 1999

i. Select City and look at Median Household Income (dollars)

j. Repeat for all of the cities from above

Chapter 11: Multiple Regression

Chapter Objectives (course):

Comparing many group means.
Analysis of Variance model.
F-Test.
Inference procedures for comparing group means

Population multiple regression equation, Multiple linear regression model, Estimation of the multiple regression parameters, Confidence intervals and significance tests for regression coeffients, ANOVA table for multiple regression, Squared multiple correlation R^2, Preliminary analysis, Residuals, Regression using all variables, Multiple logistic regression.

Objective (civic learning):

1. For your state:

A. Run the multiple linear regression using Year, Total Part I Offenses, and Total Part II Offenses to predict Burglary. Give the fitted regression equation.
B. Give the null and alternative hypotheses for the ANOVA F test. Report the results of this test, giving the test statistic, degrees of freedom, P-value, and conclusion.

C. What percent of the variation in Burglary is explained by this multiple regression?
D. Summarize the results of the significance tests for the individual regression coefficients.
E. Analyze the residuals and summarize your conclusions.

To get the correct data, use the following steps:

a. Go to the web site http://www.mnplan.state.mn.us/datanetweb/

b. Select Justice Profiles

c. Select Arrests and Apprehensions

d. Under Select Area, and select State of Minnesota

e. Highlight or select all of the years available (1985 to 1999).

1. For your county:

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Justice Profiles
Select Arrests and Apprehensions
Under Select Area, select County, and then select your county
Highlight or select all of the years available (1985 to 1999).

Chapter 12: One-Way Analysis of Variance

Chapter Objectives (course):

Comparing means, The two-sample t statistic, ANOVA hypothesis, ANOVA model, Estimates of population parameters, Testing hypothesis in one-way ANOVA, The F test, Multiple comparisons, Software, Power.

Objective (civic learning):

Data Information:

12.1: http://www.mnplan.state.mn.us/datanetweb/

1. For the State of Minnesota:
A. Make a table of means and standard deviations for the three different time periods, and plot the means.
B. State H_o and H_a for an ANOVA on these data, and explain in words what ANOVA tests in this setting.
C. Using computer software, run the ANOVA. What is the F statistic and it’s P-value? Give the values of s_p and r². What do you conclude?

State of Minnesota

Time Period	Total Vandalism
1985 to 1989	5647	5693	5524	5647	5634
1990 to 1994	7163	6505	7181	7454	8430
1995 to 1999	8344	8573	8269	8799	8115

Table 12.1: Time Period by Total Vandalism for the state of Minnesota.

1. For your county:

A. Make a table of means and standard deviations for the three different time periods, and plot the means.
B. State Ho and Ha for an ANOVA on these data, and explain in words what ANOVA tests in this setting.
C. Using computer software, run the ANOVA. What is the F statistic and it’s P-value? Give the values of Sp and R^2. What do you conclude?

To get the correct data, use the following steps:

a. Go to the web site http://www.mnplan.state.mn.us/datanetweb/

b. Select Justice Profiles

c. Select Arrests and Apprehensions

d. Under Select Area, select County

e. Select your county

f. Highlight or select all of the years available (1985 to 1999)

g. Under Part II Offenses, look at Total Vandalism

h. Scroll down to get all of the data.

Chapter 13: Two-Way Analysis of Variance

Chapter Objectives (course):

The two-way ANOVA model, The ANOVA table for two-way ANOVA.

Objective (civic learning):

1. For the state of Minnesota:

The means for the number of cases of Smoking & Tobacco Use are:

Group	1994	1996	1999
Smoking & Tobacco Use (9^th Grade)	12.4	17.5	20.5
Smoking & Tobacco Use (12^th Grade)	22.4	26.0	34.0

Table X: Means for the number of cases of Smoking & Tobacco Use (9^th Grade) and Smoking & Tobacco Use (12^th Grade) for the state of Minnesota with year.

* Number of cases per 100

A. Plot the group means with year on the x axis and number of cases of smoking & tobacco use on the y axis. For each group connect the points for the different year.
B. Describe the patterns you see. Does there appear to be a difference between the two groups? Does smoking & tobacco use appear to vary with year? If so, how does it vary? Is there an interaction between group and year?
C. Compute the marginal means. Find the differences between the Smoking & Tobacco Use (9^th) and Smoking & Tobacco Use (12^th) mean number of cases for each group. Use this information to summarize numerically the patterns in the plot.

1. For each county in your region, determine the mean for the number of cases of Smoking & Tobacco Use for 9^th and 12^thgrade.

A. Plot the group means with year on the x axis and number of cases of smoking & tobacco use on the y axis. For each group connect the points for the different year.
B. Describe the patterns you see. Does there appear to be a difference between the two groups? Does smoking & tobacco use appear to vary with year? If so, how does it vary? Is there an interaction between group and year?
C. Compute the marginal means. Find the differences between the Smoking & Tobacco Use (9^th) and Smoking & Tobacco Use (12^th) mean number of cases for each group. Use this information to summarize numerically the patterns in the plot.

To get the correct data, use the following steps:

Go to the web site http://www.mnplan.state.mn.us/datanetweb/
Select Children’s Report Card
Under Select Area, select County
Select your county
Under Children's Report Card Trend Line for Selected Indicator(s), scroll down to Smoking & Tobacco Use (9^thgrade) and Smoking & Tobacco Use (12^thgrade)
Highlight both indicators and press on Enter Choice.

Chapter 14: Nonparametric Tests

Chapter Objectives:

Section 14.1. Wilcoxon Rank Sum Test

Technique:

The rank transformation, The Wilcoxon rank sum test, The normal approximation.

Objective (civic learning)

Section 14.2. The Wilcoxon Signed Rank Test

Technique:

Objective (civic learning):

Section 14.3. The Kruskal-Wallis Test

Technique: The Kruskal-Wallis test.

Objective (civic learning):

Chapter 15: Logistic Regression

Chapter Objectives (course):

Technique :

Binomial distributions and odds, Inference for logistic regression, Multiple logistic regression.

Objective (civic learning):