MATH. 3611
SPRING, 1999
COURSE WEB SITE	http://mnstats.morris.umn.edu//introstat/
# OF CREDITS :	4
PREREQUISITE:	MATH. 3610 OR #
DAYS & TIME:	11:00-11:50
BUILDING & ROOM:	SS. 124

INSTRUCTOR:	Dr. Engin A. Sungur
OFFICE:	253 SCIENCE
TELEPHONE:	x6325
OFFICE HOURS:	MTWThF, 1-2
E-Mail	sungurea@caa.morris.umn.edu

COURSE DESCRIPTION: The topics from Mathematical Statistics such as; survey sampling, estimation of parameters and fitting probability distributions, Testing hypothesis and assessing goodness of fit, summarizing data, comparing two sample, the analysis of variance, linear least squares will be covered. Data analytical approach to mathematical statistics will be followed. MINITAB and SYSTAT computer statistical packages will be used.
GOALS OF THE COURSE:

1. Learn to understand the main features of traditional and modern statistics.
2. Learn how to analyze statistical data properly.
3. To understand the role of formal statistical theory and informal data analytic methods.
4. Gain an understanding of statistical methods relevant to upper division interdisciplinary courses.
5. To prepare students to the jobs that involve statistical analysis of data.
6. To understand the relation and balance between the theory and application.

COURSE MATERIALS: (i) John A. Rice, Mathematical Statistics and Data Analysis (Second Edition), Wadsworth and Brooks/Cole Statistics/Probability Series, 1995 (The text book is the most recent and comprehensive book in this area. The author believes that separating theory and data analysis is artificial, so the textbook provides a nice balance between theory and practice. It can be used as a source book. Its wide and updated coverage makes it a good investment.)

(ii) Study Guide

EXAMINATION POLICY: Two midterm examinations and a final exam will be given. Time table for the examinations is given below:

MIDTERM 1	APRIL, 20 (Tuesday)	SS. 124	11:00-11:50
MIDTERM 2	MAY, 20 (Thursday)	SS. 124	11:00-11:50
FINAL	JUNE, 10 (Tuesday)	SS. 124	9:30-11:30

EACH EXAMINATION (INCLUDING THE FINAL) WILL BE CLOSED-BOOKS AND CLOSED-NOTES.

HOMEWORKS: Eight homeworks will be assigned. No late homeworks will be accepted without a valid excuse. Solutions will be available at the following class.

COURSE GRADE:

HOMEWORKS:	20%
MIDTERM EXAMS:	50%
FINAL EXAM:	30%

PLEASE FEEL WELCOME TO SEE ME OUTSIDE OF THE CLASS, ANY TIME, IF YOU HAVE QUESTIONS, PROBLEMS, OR COMMENTS PERTAINING THE COURSE WORK.

The detailed syllabus of the course is given in the following table.

	READINGS
I. DISTRIBUTIONS DERIVED FROM THE NORMAL DISTR.;	RICE, 177
II. SURVEY SAMPLING;	RICE, 185
III. ESTIMATION;	RICE, 239
IV. HYPOTHESIS TESTING;	RICE, 299
V. SUMMARIZING DATA;	RICE, 345
VI. COMPARING TWO SAMPLE;	RICE, 387
VII. ANALYSIS OF VARIANCE;	RICE, 443
VIII. LINEAR LEAST SQUARES;	RICE, 507

The organization of the in-class activities are summarized in the following flowchart. The main components of the organization structure are:

(i) Summaries and Outline: These two components, hopefully, will provide a smooth transition between the topics and lectures. These will answer three basic questions: Where have we been?, Where are we going?, and What have we learned?

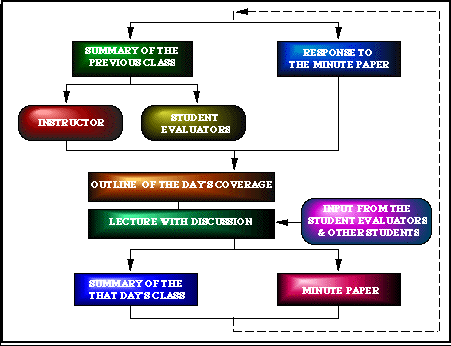
(ii) Student Evaluators: Class participation and discussion are very important on the learning process. Students are encouraged to ask questions in the class. Questions, comments could help the instructor to set up his/her pace. The input from the students should be constant. If you point out the weaknesses of the instructor, and the problems with the course in general as soon as possible your learning process will be enhanced. To formalize and promote active learning, each in-class activity will be evaluated by the two students. These students will be responsible to point out all the problems that might affect the learning of the rest of the class. For example, the topics that are not clearly covered, pace of the lecture, use of the blackboard, problems with taking notes, etc.Time to time student evaluators will be asked to make a summary of the previous class.

(iii) Minute paper: Time to time you will be asked to answer the following three questions:

1. What was the most important thing you learned today?

2. What was the most important thing you learned yesterday?

3. What questions are uppermost in your mind as we conclude this class session?

Answers to these questions will help the instructor on setting up her/his pace, pin-point the topics that the students are having problems on understanding, to correct misunderstanding etc. The questions are related with effectiveness of the lecture, retention of the information delivered, and effectiveness of the teaching in general.

The topics that will be covered are mostly in the text book. If a topic is not in your textbook, then it will be pointed out in the lecture and/or handouts will be provided.

Exams will cover the material discussed in the class and the readings in the text. Before the exam, an information sheet will be provided. This information sheet (worksheet) will include (a) place and date of the examination, (b) the detailed topics that will be covered in the examination, (c) the tools that students must bring to the examination (such as statistical tables, calculators etc.). One day before the exam, the topics that will be included in the exam will be reviewed, and important points that should be remembered will be pointed out. Right after the examination, the students will get the solutions. The anticipated grading time of the exams is 1 day.

The students should plan on taking the exam on the scheduled date. Illness (Health Service Excuse) or a Chancellor's excuse will be honored as a reason for taking the exam at other than the scheduled date. (Make-ups creates a data which is not independent and identically distributed. As you will learn in this course, lack of these properties creates a big problem on the inference based on such data).

No late homeworks will be accepted without a valid excuse.

The difficulty of the exams will be so arranged that there will be no need for the "normalization" of the scores based on the Gaussian Distribution (known as making a curve). Trends on the scores, attendance to the lectures, class participation etc. will be considered on the determination of the final grades.