MATH. 3610
WINTER, 1999
COURSE WEB SITE	http://mnstats.morris.umn.edu//introstat/
# OF CREDITS :	4
PREREQUISITE:	MATH. 1202 OR 1302 OR #
DAYS & TIME:	10:00-10:50
BUILDING & ROOM:	SS. 136

INSTRUCTOR:	Dr. Engin A. Sungur
OFFICE:	253 SCIENCE
TELEPHONE:	x6325
OFFICE HOURS:	MTWThF, 1-2
E-Mail	sungurea@caa.morris.umn.edu

COURSE DESCRIPTION: The course will concentrate on Probability Theory and Statistical Methods. Probability theory; set theory, axiomatic foundations, conditional probability and independence, Bayes's Rule, random variables. Transformations and expectations; expected values, moments and moment generating functions. Common families of distribution; discrete and continuous distributions. Multiple random variables; joint and marginal distributions, conditional distributions and independence, covariance and correlation, multivariate distributions. Properties of a random sample and central limit theorem. Markov chains, Poison processes.

COURSE MATERIALS: (i) Sheldon, M. R., Introduction to Probability Models (sixth edition), Academic Press, 1993

(ii) Study Guide

EXAMINATION POLICY: Two midterm examinations and a final exam will be given. Time table for the examinations is given below:

MIDTERM 1	JANUARY, 26 (Tuesday)	SS. 136	10:00-10:50
MIDTERM 2	FEBRUARY, 25 (Thursday)	SS. 136	10:00-10:50
FINAL	MARCH, 16 (Tuesday)	SS. 136	9:30-11:30

EACH EXAMINATION (INCLUDING THE FINAL) WILL BE CLOSED-BOOKS AND CLOSED-NOTES.

HOMEWORKS: Eight homeworks will be assigned. No late homeworks will be accepted without a valid excuse. Solutions will be available at the following class.

COURSE GRADE:

HOMEWORKS:	20%
MIDTERM EXAMS:	50%
FINAL EXAM:	30%

PLEASE FEEL WELCOME TO SEE ME OUTSIDE OF THE CLASS, ANY TIME, IF YOU HAVE QUESTIONS, PROBLEMS, OR COMMENTS PERTAINING THE COURSE WORK.

The detailed syllabus of the course is given in the following table.

TOPIC	TEXT BY ROSS	STUDY GUIDE
Introduction & Sample Space and Events	§ 1.1-1.2	§ I.1-I.2 § I.3
Probabilities	§ 1.3	§ I.4-I.5
Conditional Probabilities	§ 1.4	§ I.5
Independent Events	§ 1.5	§ I.5
Bayes' Formula	§ 1.6	§ I.5
Random Variables	§ 2.1	§ II.2-II.3
Discrete Random Variables	§ 2.2	§ II.1 Discrete Mathematics, Binomial Theorem, Geometric Series, Maclaurin Series
Continuous Random Variables	§ 2.3	§ II.1 The Derivative of a Function, Derivatives of the Composite Functions, The Definite Integral, Antidifferentiation, Evaluation of the Integrals, Methods of Integration, Some Special Functions
Expectation of a Random Variable	§ 2.4	§ II.1 Evaluation of the Definite Integrals by Using Antiderivatives, Methods of Integration
Jointly Distributed Random Variables	§ 2.5	§ II.1 Some Results Involving Multivariate Calculus
Moment Generating Functions	§ 2.6	§ II.1 Methods of Integration, Some Results Involving Limits
Limit Theorems	§ 2.7	§ II.1 Some Results Involving Limits
Conditional Probability & Conditional Expectation	Chapter 3	§ II.1
Markov Chains	Chapter 4	§ I.6 & II.1
The Exponential Distribution & the Poisson Process	Chapter 5	§ II.1

The organization of the in-class activities are summarized in the following flowchart. The main components of the organization structure are:

(i) Summaries and Outline: These two components, hopefully, will provide a smooth transition between the topics and lectures. These will answer three basic questions: Where have we been?, Where are we going?, and What have we learned?

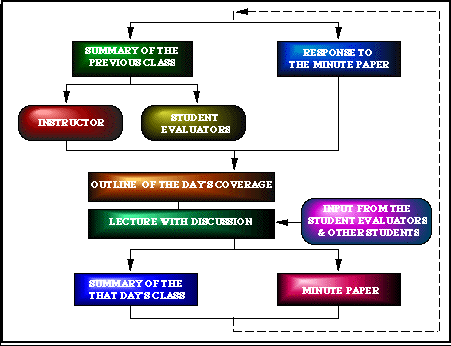
(ii) Student Evaluators: Class participation and discussion are very important on the learning process. Students are encouraged to ask questions in the class. Questions, comments could help the instructor to set up his/her pace. The input from the students should be constant. If you point out the weaknesses of the instructor, and the problems with the course in general as soon as possible your learning process will be enhanced. To formalize and promote active learning, each in-class activity will be evaluated by the two students. These students will be responsible to point out all the problems that might affect the learning of the rest of the class. For example, the topics that are not clearly covered, pace of the lecture, use of the blackboard, problems with taking notes, etc.Time to time student evaluators will be asked to make a summary of the previous class.

(iii) Minute paper: Time to time you will be asked to answer the following three questions:

1. What was the most important thing you learned today?

2. What was the most important thing you learned yesterday?

3. What questions are uppermost in your mind as we conclude this class session?

Answers to these questions will help the instructor on setting up her/his pace, pin-point the topics that the students are having problems on understanding, to correct misunderstanding etc. The questions are related with effectiveness of the lecture, retention of the information delivered, and effectiveness of the teaching in general.

The topics that will be covered are mostly in the text book. If a topic is not in your textbook, then it will be pointed out in the lecture and/or handouts will be provided.

Exams will cover the material discussed in the class and the readings in the text. Before the exam, an information sheet will be provided. This information sheet (worksheet) will include (a) place and date of the examination, (b) the detailed topics that will be covered in the examination, (c) the tools that students must bring to the examination (such as statistical tables, calculators etc.). One day before the exam, the topics that will be included in the exam will be reviewed, and important points that should be remembered will be pointed out. Right after the examination, the students will get the solutions. The anticipated grading time of the exams is 1 day.

The students should plan on taking the exam on the scheduled date. Illness (Health Service Excuse) or a Chancellor's excuse will be honored as a reason for taking the exam at other than the scheduled date. (Make-ups creates a data which is not independent and identically distributed. As you will learn in this course, lack of these properties creates a big problem on the inference based on such data).

No late homeworks will be accepted without a valid excuse.

The difficulty of the exams will be so arranged that there will be no need for the "normalization" of the scores based on the Gaussian Distribution (known as making a curve). Trends on the scores, attendance to the lectures, class participation etc. will be considered on the determination of the final grades.