
|

|
5. From Probability to Inference
5.1 Counts and Proportions
Understanding what a binomial experiment is
Checking the assumptions of a binomial experiment
How to use binomial tables to find probabilities
Finding mean and variance of counts under binomial experiment
Understanding the difference between sample and population proportion
Understanding the connection between counts and sample proportions
Finding sample proportion probabilities by using binomial tables
Finding the mean and variance of sample proportions
Finding count and sample proportion probabilities by using normal approximation
5.2 Sample Means
Understanding the difference between population mean and sample mean
Finding the mean and standard deviation of the sample mean
Being able to apply central limit theorem
To be able to solve problems related with this section, first of all you should be able to see whether the problem related with proportions or means.
This is what we mean when we say count:
X=the number of times an event occurs in fixed number of trials.
or
X=count of occurrences of some outcome in fixed number of observations
n=fixed number of observations(trials)
This is what we mean when we say sample proportion:
p^=sample proportion=X/n.
|
Observation (Trial) |
Success |
Failure |
p |
n |
X |
|
Tossing a fair coin |
Head |
Tail |
1/2 |
Number of tosses |
Number of Heads in n tosses |
|
Birth of a child |
Girl |
Boy |
Practically 1/2 |
Fixed family size |
Number of girls in a family of size n |
|
Throwing two dice |
7 dots |
Anything else |
6/36 |
Number of throws |
Number of sevens in n throws |
|
Inspecting a product |
Non-defective |
Defective |
Proportion of defectives in the population |
Sample size |
Number of non-defectives in a sample of size n |
|
Asking a question |
Correct answer |
Wrong answer |
Probability of giving a correct answer |
Number of questions asked |
Number of correct answers out of n questions |
Since p=0.8 is not on the table we should do something else.
Note that X="Number alive at age 65 out of 10" has a Binomial distribution with n=10 and p=0.8.
Now switch the definition of the sucess with the failure. In other words, count the number not alive instead of alive.
In this case we start to work with
Y="Number not alive at age 65 out of 10".
the value of X automatically determines the value of Y. For example if X=2 (number of alive out of 10 is 2), then Y=8 (number not alibe out of 10).
So, Y will have a Binomial distribution with n=10 but p=0.2.
and P(X=2)=P(Y=8).
Now try to find P(Y=8) by using Table C.
| If X had a Binomial
distribution with n and p, then
Mean of X=mX=np Standard Deviation of X=sX =Square Root of np(1-p) |
Using the formula First let us get familiar with the formula to find the probability of obtaining k successes out of n trials, that is P(X=k).
P(X=k)=

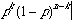
Suppose that someone who visits a car dealer purchases a car with
probability 0.2. The dealer has 8 cars in stock. On that day 10 people
visits the dealership. What is the probability that the dealership run
out of stock?
In this case the variable of interest is X=Number of puchases by 10 visitors.
X has a Binomial distribution with n=10 and p=0.2
The dealership will run out of stock if more than 8 visitors out of 10 decides to purchase a car. Therefore:
P("out of stock")=P(X>8)=P(X=9)+P(X=10)
Now we can use the formula:
P(X=k)=

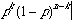 to find P(X=9) and P(X=10).
to find P(X=9) and P(X=10).
For P(X=9) n=10 k=9 and p=0.2
Similarly, P(X=10)=0.000000102.
Therefore P(X>8)=0.00000409+0.000000102=0.000004192.
Suppose that we want to get an idea on the proportion of the people who really find what they are looking for on the WEB. Since we can not reach all the people who are using WEB, we take a sample of size n and ask them whether or not they found what they were looking for on WEB.
Here is the explanation of the notations that we are using:
p=the proportion of the people who really find what they are looking for on the WEB (this is called a parameter and it is unknown)
p^=the proportion of the n people that we sampled who found what they were looking for (statistics, estimator of the unknown p).
X=the number of people in the sample(n people) who found what they were looking for.
n=sample size.
Note that p^=X/n=(number of successes in a sample of n)/(sample size)
Here the "success" is "finding what s/he looking for on the WEB".
We have learned that X has a binomial distribution with n and p.
How can we find a probability related with a proportion? For example, what is the probability that the proportion of people who found what they want in my sample is more than 50%?
To answer these type of questions we should translate p^>0.50 into an event interms of X and use the knowledge that we have gained on how to find Binomila probabilities.
P(p^>0.50)=P(X/n>0.50)=P{X>n(0.50)}
Suppose that we interviewed 100 people and p=0.80, then
P(p^>0.50)=P(X/100>0.50)=P{X>100(0.50)}=P(X>50)
Observe that if the proportion of people who found what they want is
more than 50% in the sample of size 100, then out of 100 more than 50 of
them found what they were looking for.
| If X had a Binomial
distribution with n and p, then
Mean of p^=mp^=p Standard Deviation of p^=sp^ =Square Root of p(1-p)/n |
Please compare the above properties of p^(sample proportion) with the
properties of the X(count)
| If X had a Binomial
distribution with n and p, then
Mean of X=mX=np Standard Deviation of X=sX =Square Root of np(1-p) |
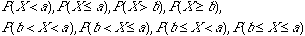
OR
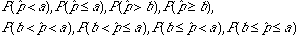
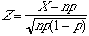
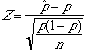
Example (Checking for Undercoverage in Surveys:One way of checking the effect of undercoverage, and other sources of error in a sample survey is to compare the sample with known facts about the population.The fact that we are going to use in this example is about 11% of the American adults are African Americans The proportion, p^, of African American in a simple random sample of 1,500 adults should therefore be close to 11%. It is unlikely to be exactly 11% because of the sampling variability. If a national survey contains only 9.2% African Americans, should we suspect that the sampling procedure is somehow underrepresenting African Americans?
|
The following are some interesting links that you may want to try.
|
Population |
Sample |
|
Characteristics that you are interested X |
You decide to get n individuals from this population and get the value of the characteristics that you are interested X 1, X2, ..., Xn |
|
Average value(mean) of the characteristic m |
To get an idea on unknown population mean, you average your n observations
The sample mean
|
|
Standard deviation of the characteristic s |
The sample standard deviation has the following standard deviation:
|
|
For the population the characteristic has a normal distribution. That is, if you get the value of this characteristics from all the individuals in your population and produce a graphical display such as stemplot or histogram it appears to be bell shaped. |
If the characteristic has a Normal distribution then
|
|
For the population you do not have a slightest idea what the shape of the distribution is. |
If you have a large enough sample, then
This result is known as the CENTRAL LIMIT THEOREM |
| SECTION 5.1.Exercise 5.3, 5.7, 5.8, 5.12, 5.14 (page 391-394) |
| SECTION 5.2.Exercises 5.25, 5.30, 5.40 (pages 408-413) |
| CHAPTER EXERCISES.Exercises 5.68 (page 429) |