UNIVERSITY OF MINNESOTA, MORRIS

INTRODUCTION TO STATISTICS

(GENED WEB)

MATH. 1601

SOLUTIONS TO THE PRACTICE TEST

FALL, 1999

FOR INSTRUCTOR'S USE

1.							........../10
2.	a........./5	b........./5	c........./5	d........./5	e........./5	f........./5	........../30
3.							........../10
4.	a........./10	b........./10					........../20
5.							........../10
6.	a........./5	b........./5	c........./5	d........./5			........../20
7.	a........./5	b........./5					........../10
8.							........../10
9.	a........./5	b........./5	c........./5				........../15
10.	a........./8	b........./7					........../15

TOTAL							........../150

1. A telemarketing firm in Los Angeles uses a device that dials residential telephone numbers in that city at random. Of the first 100 numbers dialed 43 are unlisted. This is not surprising, because 52% of all residential phones are unlisted.

What is the parameter?, What is the statistic?

ANSWER 1:

parameter is the proportion of unlisted residential telephone numbers in Los Angeles which is 52%.

statistic is the proportion of unlisted residential telephone numbers in the sample. The value of the statistic is 43%.

2. Mothers Against Drunk Driving is a very visible group whose main focus is to educate the public about the harm caused by drunk driving. In a recent study the number of vehicles involved and whether alcohol played a role in the accident were noted. The following table provides the associated probabilities.

Did Alcohol Play a role?	Number of Vehicles Involved
Did Alcohol Play a role?	1	2	3
Yes	0.1250	0.2500	0.0500
No	0.0625	0.4375	0.0750

Assume that you selected one of these accidents at random.

a. What is the probability that the accident involved more than a single vehicle?

b. What is the probability that the accident involved alcohol or a single car?

c. What is the probability that the accident involved alcohol, given that accident involved a single vehicle?

d. What is the probability that the accident involved a single vehicle, given that it involved alcohol?

e. Are the events "number of vehicles involved is 1" and "number of vehicles involved is 3" disjoint? Are they independent? Please justify your answer to receive a credit.

f. Are the events "the accident involved a single car" and "the accident involved alcohol" independent? Are they disjoint? Please justify your answer to receive a credit.

ANSWER 2:

Let

A="yes"

B="no"

C="1 vehicle involved"

D="2 vehicles involved"

E="3 vehicles involved"

a. P(D or E)=P(D)+P(E)=0.2500+0.0500+0.4375+0.0750=0.8125

b. P(A or C)=P(A)+P(C)-P(A and C)=0.425+0.1875-0.125=0.4875

c. P(A|C)=P(A and C)/P(C)=0.125/0.1875=0.667

d. P(C|A)=P( A and C)/P(A)=0.125/0.425=0.294

e. C and E can not occur at the same time. Therefore they are disjoint.

P(C and E)=0, but P(C)xP(E)=(0.1875)x(0.1250)=0.0234375.

Since P(C and E) is not equal to P(C)P(E) they are not independent. Since C and E can occur at the same time, they are not disjoint

3. Suppose we wish to learn what proportion of the population has a certain, slightly kinky, sexual practice. This is a sensitive enough issue that a randomized survey is proposed. The subject tosses a coin, and if the toss is heads they answer the sex question. If the first toss is a tails, they toss a coin again, and if the next toss is heads they answer "yes", if the next toss is tails they answer "no". There were 77 subjects, and there were 27 "yes" answers to the survey. Give an estimate of the proportion of the population that has the kinky sexual practice?

ANSWER 3:

Let

H="getting a head"

T="getting a tail"

Y="answer being yes"

N="answer being no"

Here is the tree diagram for this:

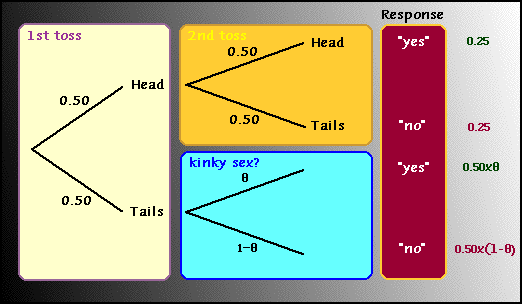
P("yes")=0.25+0.50xq

In the sample the estimate of the P("yes") is 27/77=0.35.

Therefore,

0.25+0.50xq will be approximately 0.35

0.25+0.50xq =0.35

q =(0.35-0.25)/0.50=0.20.

a. A Harris poll found that 46% of Americans say they suffer great stress at least once a week. If three people are selected at random, find the probability that all three will say that they suffer stress at least once a week.

b. The probability that Sam parks in a no-parking zone and gets a parking ticket is 0.06, and the probability that Sam cannot find a legal parking space and has to park in the no-parking zone is 0.20. On Tuesday, Sam arrives at school and has to park in a no-parking zone. Find the probability that he will get a parking ticket given that he parked in a no-parking zone.

ANSWER 4:

a. X=Number of people who suffer great stress at least once a week out of three.

X has a binomial distribution with n=3 and p=0.46.

b. Let

A=parking an a no-parking zone

B=getting a ticket

P(A and B)=0.06

P(A)=0.20

P(B|A)=P(A and B)/P(A)=0.06/0.20=0.30.

5. A UMM student goes to a casino and wishes to play either game A or game B. Game A costs $2 and has a probability of winning $6 of 0.3. Game B costs $1 and has a probability of winning $3 of 0.3. Which game should the student play if s/he wishes to maximize the expected net gain?

ANSWER 5:

For Game A:

Expected Gain=(6x0.3+0x0.7)-2=1.8-2=-0.2

For Game B:

Expected Gain=(3x0.3+0x0.7)-1=0.9-1=-0.1.

S/he should play Game B.

6. The probability distribution for the number of toppings, in addition to cheese, ordered on a pizza is

x	0	1	2	3	4
probability	0.3	0.4	0.2	0.06	0.04

a. Determine the mean and the standard deviation.

b. What is the probability that a customer will not order any topping?

c. Find P(1<x<4).

d. If a customer orders at least one topping, what is the probability that s/he will order 2 toppings?

ANSWER 6:

a. Mean= 0(0.3)+1(0.4)+2(0.2)+3(0.06)+4(0.04)=1.14

Variance=(0-1.14)²(0.3)+(1-1.14)²(0.4)+(2-1.14)²(0.2)+(3-1.14)²(0.06)+(4-1.14)²(0.04)

=0.38988+0.00784+0.14792+0.207576+0.327184=1.0804

Standard deviation=1.0394

b. P(X=0)=0.3

c. P(1<X<4)=P(X=2)+P(X=3)=0.26

d. P(X=2|X>0)=0.2/0.7=0.2857

7. 70% of the light aircraft that disappear while in flight in a certain country are subsequently discovered. Of the aircraft that are discovered, 60% have an emergency locator, whereas 90% of the aircraft not discovered do not have such a locator.

a. Find the probability that a light aircraft has an emergency locator.

b. Find the probability that aircraft will be discovered given that it has an emergency locator.

ANSWER 7:

Let

A=aircraft discovered

B=aircraft has emergency locator

P(A)=0.70

P(B|A)=0.60

P(B^c|A^c)=0.90

a. P(B)=P(B|A)P(A)+P(B|A^c)P(A^c)=0.60(0.70)+0.10(0.30)=0.42+0.03=0.45

b. P(A|B)=P(A and B)/P(B)=(0.6x0.7)/0.45=0.9333.

8. Econo-Jet airlines sells 8 tickets for each of their small plane flights. The probability of any ticketholders showing up for a flight is 0.3. Assume that ticketholders arrive for flights independently. The airplanes have five seats. What is the probability that too many ticketholders show up for the flight and some ticketholders will have to be left behind to take a later flight?

ANSWER 8:

Let

X=Number of 8 ticketholders who will show up.

X has a binomial distribution with n=8 and p=0.30.

P(X>5)=P(X=6)+P(X=7)+P(X=8)=0.0100+0.0012+0.0001=0.0113

9. Suppose an opinion poll of 140 UMM Campus Assembly members found that 60 of them supported a change to the UMM constitution. We are interested in the true proportion p that support this change to the UMM constitution.

a. What is the best estimate of the p?

b. Suppose the true proportion of voters that support this change is 0.666. What is the probability of observing a sample proportion less than 60/140 from a sample of 140?

c. Based on the results of this study, do you think the constitution change will pass? The change passes if more than or equal to 66.6% vote "yes".

ANSWER 9:

a. p^=60/140=0.42857

b. p=0.666

P(p^<0.42857)=P(Z<(0.42857-0.666)/0.03986))=P(Z<-5.96)

which is almost 0.

c. It is very unlikely that it will pass.

10. An automobile insurance company estimates the following loss probabilities for the next year on a $25,000 sports car:

Total loss: 0.001

50% loss: 0.01

25% loss: 0.05

10% loss: 0.10.

Assuming the company will sell only a $500 deductible policy for this model (i.e., the owner covers the first $500 damage).

a. Find the probability distribution of x=amount paid on the sports car loss.

b. If the insurance company charges an annual premium of $1007, what is the company's average profit?

ANSWER 10:

a.

Amount Paid, x	Probability, p
$25,000	0.001
$12,500	0.01
$6,250	0.05
$2,500	0.10
$0	0.839

b. Average Profit=$1007-(Average of X)

Average of X=$25,000(0.001)+$12,500(0.01)+$6,250(0.05)+$2,500(0.10)+$0(0.839)

=$712.50

Average Profit=$1007-$712.50=294.50